Зіставлення емпіричного розподілу з теоретичним

Обмеження критерію l

Опис критерію

Призначення критерію

Критерій l призначений для співставлення двох розподілів:

а) емпіричного з теоретичним, наприклад, рівномірним або нормальним;

б) одного емпіричного розподілу з іншим емпіричним розподілом.

Критерій дозволяє найти точку, в якій сума накопичених відмінностей між двома розподілами є найбільшою, і оцінити достовірність цих відмінностей.

Якщо в методі χ² ми зіставляли частоти двох розподілів окремо по кожному розряду, то тут співставляються спочатку частоти за першим розрядом, потім за сумою першого та другого розрядів, потім за сумою першого, другого та третього розрядів і т.п. таким чином, ми зіставляємо кожного разу накопичені до даного розряду частоти. Якщо відмінності між двома розподілами суттєві, то в якийсь момент різниця накопичених частот досягне критичного значення, і ми зможемо визнати відмінності статистично достовірними. Формула критерію l містить цю різницю. Чим більше емпіричне значення l, тим більш суттєві відмінності.

1. Критерій вимагає, щоб вибірка була достатньо великою. При зіставленні двох емпіричних розподілів необхідно, щоб n _1,2≥50. Зіставлення емпіричного розподілу з теоретичним іноді допускається при n ≥5.

2. Розряди повинні бути упорядковані за зростанням або убуванням якоїсь ознаки. Вони обов’язково повинні відображати якусь одно направлену її зміну. (наприклад дні тижня, 1-й, 2-й, 3-й місяці після проходження курсу терапії, підвищення температури тіла).

Отже, ми не можемо накопичувати частоти за розрядами, які відрізняються лише якісно і не є шкалами порядку.

У всіх випадках коли розряди мають неупорядкований за зростанням або убуванням якоїсь ознаки категорії, нам слід використовувати метод χ².

У вибірці здорових осіб чоловічої статі, студентів технічних і воєнно-технічних вузів у віці від 19-ти до 22 років, середній вік 20 років, проводився тест Люшера в 8-колірному варіанті. Установлено, що жовтому кольору надають перевагу досліджувані частіше, ніж відхиляють. Чи можна стверджувати, що розподіл жовтого кольору за 8-ма позиціями у здорових досліджуваних відрізняється від рівномірного розподілу?

Розряди	Позиції жовтого кольору	сума
Емпіричні частоти

Н₀: емпіричний розподіл жовтого кольору за восьма позиціями не відрізняється від рівномірного розподілу.

Н₁: емпіричний розподіл жовтого кольору за восьма позиціями відрізняється від рівномірного розподілу.

Розрахунок критерію при співставленні розподілу виборів жовтого кольору з рівномірним розподілом (n=102)

Позиція жовтого кольору	Емпірична частота	Емпірична частість	Накопичена емпірична частість	Накопичена теоретична частість	різниця
		0,235	0,235	0,125	0,110
		0,147	0,382	0,250	0,132
		0,128	0,510	0,375	0,135
		0,078	0,588	0,500	0,088
		0,147	0,735	0,625	0,110
		0,098	0,833	0,750	0,083
		0,088	0,921	0,875	0,046
		0,079	1,000	1,000	0,000
Суми		1,000

Заносимо в таблицю найменування (номери) розрядів та відповідні емпіричні частоти.

Розраховуємо емпіричні частості f ⃰ за формулою:

f⃰=f_i/n

де f_i – частота попадання жовтого кольору на дану позицію;

n – загальна кількість спостережень;

i – номер позиції по порядку.

f⃰₁= 24/102=0,235

f⃰₂= 15/102=0,147

f⃰₃= 13/102=0,128

f⃰₄= 8/102=0,078

f⃰₅= 15/102=0,147

f⃰₆= 10/102=0,098

f⃰₇= 9/102=0,088

f⃰₈= 8/102=0,079

Підраховуємо накопичені емпіричні частостіƩ f⃰.

Ʃ f⃰ ₁ = 0,235

Ʃ f⃰ ₁₊₂ = 0,235+0,147=0,382

Ʃ f⃰ ₁₊₂₊₃ = 0,235+0,147+0,128=0,510

Ʃ f⃰ _1+2+3+4 = 0,235……………=0,588

Ʃ f⃰ _1+2+3+4+5 = 0,235………….=0,735

Ʃ f⃰ _1+2+3+4+5+6 = 0,235………..=0,833

Ʃ f⃰ _{1+2+3+4+5+6+7} = 0,235………=0,921

Ʃ f⃰ _{1+2+3+4+5+6+7+8} = 0,235…….=1,000

Необхідно визначити теоретичні частості f⃰_теор= 1 /k =1/8=0,125

k – кількість розрядів

Ця теоретична частість відноситься до всіх 8-ми розрядів. Вірогідність попадання жовтого кольору на з 8-ми позицій при випадковому виборі становить 1/8, тобто 0,125.

f⃰_{т 1} = 0,125

f⃰_{т 1+2} = 0,125+0,125=0,250

f⃰_{т 1+2+3} = 0,125+0,125+0,125=0,375

Можна визначити теоретичні накопичені частості шляхом множення:

S f⃰_тi = f⃰_т · i

f⃰_т – теоретична частість;

i – порядковий номер розряду.

Тепер залишилось вирахувати різницю між емпіричними та теоретичними накопиченими частостями (стовпчик 4-й та 5-й). в 6-й стовпчик записуються абсолютні величини цих різниць, які позначаються як d.

Визначити яка з абсолютних величин різниці є найбільшою. Вона буде називатися d_max.

В нашому прикладі d_max. =0,135.

Знаходимо критичні значення d_max. при n =102 (Табл. Х)

dкр	p=0,05	p=0,01
1,36/√n	1,63/√n
1,36/10,09	1,63/10,09
	0,135	0,161

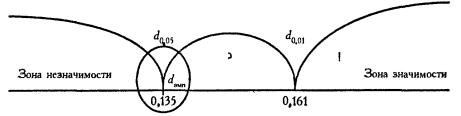
d_емп. =0,135

d_емп. = d_кр.

Висновок: Н₀ відхиляється при р =0,05. Розподіл жовтого кольору за 8-ми позиціями відрізняється від рівномірного розподілу.

Дата добавления: 2014-10-15