Рівень значимості кореляції

Деякі дослідники, обчисливши значення коефіцієнта кореляції, на цьому і зупиняються. Але з точки зору грамотної методології експерименту слід визначити і рівень значимості (тобто ступінь достовірності) даного коефіцієнта.

Рівень значимості коефіцієнта кореляції обчислюється за допомогою таблиці критичних значень. Якщо отримане в розрахунках значення r_xy перевищує критичне (табличне) значення для даної вибірки, коефіцієнт Пірсона вважається статистично значимим.

Число ступенів свободи в даному випадку відповідає df = n – 2, де n – число пар порівнюваних значень (обсяг вибірки).

r_кр = 0,707 р≤0,05

0,834 р≤0,01

Також рівень значимості можна визначати за коефіцієнтом Стьюдента, який обчислюється як відношення коефіцієнта кореляції до його помилки:

Помилка коефіцієнта кореляції вираховується за формулою:

Де m_r – помилка коефіцієнта кореляції, r – коефіцієнт кореляції, n – кількість порівнювальних пар.

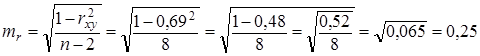
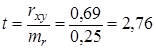
У таблиці знаходимо стандартні значення коефіцієнту Стьюдента при числі ступені свободи ν = n – 2 = 8

t_кр = 2,31 р≤0,05

3,36 р≤0,01

Висновок: кореляція між показниками є статистично значимою.

При інтерпретації коефіцієнта кореляції Пірсона необхідно враховувати наступні моменти:

1. Коефіцієнт Пірсона може використовуватися для різних шкал (шкала відносин, інтервальна або порядкова) за винятком дихотомічної шкали.

2. Кореляційний зв'язок далеко не завжди означає зв'язок причинно-наслідковий. Іншими словами, якщо ми знайшли, припустимо, позитивну кореляцію між ростом і вагою у групи досліджуваних, то це зовсім не означає, що ріст залежить від ваги або навпаки (обидві ці ознаки залежать від третьої (зовнішньої) змінної, яка у цьому випадку пов'язана з генетичними конституціональними особливостями людини).

3. r_xy ≈ 0 може спостерігатися не лише при відсутності зв'язку між x і y, а й у разі сильного нелінійного зв'язку (рис. а). У даному випадку негативна і позитивна кореляції врівноважуються і в результаті створюється ілюзія відсутності зв'язку.

4. r_xy може бути досить малий, якщо сильна зв'язок між х і у спостерігається в більш вузькому діапазоні значень, ніж досліджуваний (рис. б).

5. Об'єднання вибірок з різними середніми значеннями може створювати ілюзію досить високою кореляції (рис. в).

.. .. .. .. .. .

... . . . . . ...

.. ... + +.. + + + + +

Коефіцієнт рангової кореляції Спірмена (r_s)

Обчислення рангової кореляції дозволяє визначити силу і напрямок кореляційного зв'язку між двома ознаками, виміряними в ранговій шкалі або між двома ієрархіями ознак. При цьому по кожній змінній має бути представлено не менше п'яти спостережень. Одним з коефіцієнтів рангової кореляції є коефіцієнт Спірмена.

Коефіцієнт кореляції Спірмена (r_s) використовується в тих випадках, коли обидва ряди змінних представлені ранговими (порядковими) шкалами. Для обчислення коефіцієнта Спірмена можна користуватися двома різними формулами, які дають, в принципі, один і той же результат:

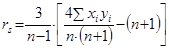
Коефіцієнт кореляції Спірмена, так само як і r_xy, може варіювати від –1 до +1. r_s = 1 тільки в тому випадку, коли ранги обох ознак в точності збігаються за х і у.

Якщо в рядах змінних (або хоча б в одному з них) є пов'язані (повторювані) ранги, то слід користуватися формулою з відповідною поправкою на пов'язані ранги:

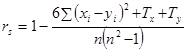
де T_x =Ʃ(x³ – x):12;

T_y =Ʃ(y³ – y):12

х – об’єм кожної групи однакових рангів в ранговому ряді х;

y – об’єм кожної групи однакових рангів в ранговому ряді у.

Приклад: у групи студентів були виміряні показники соціального інтелекту (композитна оцінка) за тестом Гілфорда і показники рівня агресивності за тестом Ассінгера. Наскільки можна ставити питання про наявність зв'язку між цими двома особистісними властивостями? Перевірка даних на нормальність розподілу показує, що вони не розподілені за кривою Гаусса. Отже, для їх обробки не можна використовувати аналіз лінійної кореляції. Дані заносяться в таблицю і переводяться з метричних значень в рангові. При цьому висуваються гіпотези:

Н₀: кореляція між показниками соціального інтелекту та рівня агресивності значимо не відрізняється від нуля (є випадковою).

Н₁: кореляція між показниками соціального інтелекту та рівня агресивності значимо відрізняється від нуля (є невипадковою).

Процедура вирахування рангової кореляції Спірмена.

№	Соціальний інтелект	Рівень агресивності	Різниця рангів	Квадрат різниці рангів
Метричні значення	Ранг	Метричні значення	Ранг
					-7
					-9
					-7
					-5
					-1
					-2
	Ʃd^2=416

Підставляючи потрібні значення в формулу, розраховуємо емпіричне значення r_s.

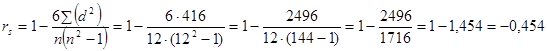
Таким чином, ми приходимо до висновку, що спостерігається помірна негативна кореляція між показниками соціального інтелекту та рівня агресивності. Рівень статистичної значущості r_s при n =12 визначається за таблицею (Табл.ХVI).

r_кр (р≤0,05) =0,58

r_кр (р≤0,01) =0,73

Для даного обсягу вибірки (n=12) мінімальне критичне значення r_s становить 0,58 при р =0,05. Тобто абсолютне значення отриманого результату знаходиться нижче самого мінімального порога статистичної значущості, і ми можемо впевнено прийняти нульову гіпотезу (r_емп<r_кр (р≤0,05)=>Н₀!). Можливо, що для отримання більш достовірних результатів слід було б збільшити об’єм вибірки.

Дата добавления: 2014-10-15