Непараметричний критерій Q Розенбаума

Класифікація критеріїв

ОЦІНКА ДОСТОВІРНОСТІ ВІДМІННОСТЕЙ

	Параметричні критерії	Непараметричні критерії
Визначення ступеню узгодженості змін (кореляція)	r (коефіцієнт кореляції Пірсона)	rs (коефіцієнт кореляції Спірмена) φ (коефіцієнт фі-кореляції Пірсона)
Порівняння розподілів		Χ^2 -(критерій відповідності)
Оцінка достовірності відмінностей	t -критерій Стьюдента для незалежних вибірок	U критерій Манна-Уїтні H -критерій Крускала-уоліса m біноміальний критерій χ^2 -(критерій однорідності)
Оцінка достовірності відмінностей при повторних вимірах	t -критерій Стьюдента для залежних вибірок	T -критерій Вілкоксона
Аналіз змін ознаки. Порівняння дисперсій	F -критерій Фішера

Завдання	Умови	Методи
1. Вияв відмінностей на рівні досліджуваної ознаки	а) 2 вибірки досліджуваних   б) 3 і більше вибірок досліджуваних	Q – критерій Розенбаума; U – критерій Манна-Уїтні; φ⃰ – критерій (кутове перетворення Фішера); S – критерій тенденцій Джонкіра; H – критерій Крускала-Уоліса.
2. Оцінка зсуву значень досліджуваної ознаки	а) 2 виміри на одній і тій же вибірці досліджуваних     б) 3 та більше вимірів на одній і тій же вибірці досліджуваних	Т – критерій Вілкоксона; G – критерій знаків; φ⃰ – критерій (кутове перетворення Фішера); χr^2 – критерій Фрідмана; L – критерій тенденцій Пейджа.
3. Вияв відмінностей в розподілі ознаки	а) при співставленні емпіричного розподілу з теоретичним	χ^2 – критерій Пірсона; λ – критерій Колмогорова-Смірнова; m – біноміальний критерій.
4. Вияв ступеню узгодженості змін (кореляція)	а) двох ознак   б) двох ієрархій або профілей	rs – коефіцієнт рангової кореляції Спірмена. rs – коефіцієнт рангової кореляції Спірмена.
5. Аналіз змін ознаки під впливом контрольованих умов	а) під впливом одного фактора     б) під впливом двох факторів одночасно	S – критерій тенденцій Джонкіра; L – критерій тенденцій Пейджа; однофакторний дисперсійний аналіз Фішера. двофакторний дисперсійний аналіз Фішера

Q -критерій Розенбаума заснований на порівнянні «накладених» один на одного ранжируваних рядів значень двох незалежних змінних. При цьому не аналізується характер розподілу ознаки всередині кожного ряду – в даному випадку має значення лише ширина ділянок, які не перекриваються двох ранжируваних рядів. При порівнянні між собою двох ранжируваних рядів змінних можливі 3 варіанти:

1. Ранжирувані ряди x і y не мають області перекриття, тобто всі значення першого рангового ряду (x) більші всіх значень другого рангового ряду (y):

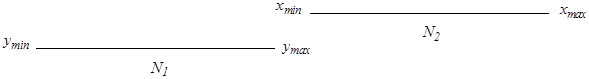
У даному випадку відмінності між вибірками, що визначаються по будь-якому статистичному критерію, безумовно достовірні, і використання критерію Розенбаума не потрібно. Проте на практиці такий варіант зустрічається виключно рідко.

2. Ранжирувані ряди повністю накладаються один на одного (як правило, один з рядів знаходиться всередині іншого), зони, які не перекриваються, відсутні. У даному випадку критерій Розенбаума непридатний.

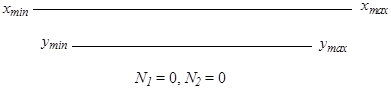
3. Мається зона перекриття рядів, а також дві області, які не перекриваються (N₁ і N₂), що відносяться до різних ранжируваних рядів (позначимо х – ряд, зсунутий у бік великих, y – у бік менших значень):

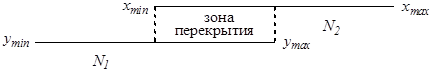
Даний випадок є типовим для використання критерію Розенбаума, при використанні якого слід дотримуватися таких умов:

1. Обсяг кожної вибірки повинен бути не менше 11.

2. Обсяги вибірок не повинні істотно відрізнятися один від одного. Критерій Q Розенбаума відповідає числу значень, які не перекриваються: Q = N₁ + N₂. Висновок про достовірність відмінностей між вибірками робиться у випадку, якщо Q > Q _кр. При цьому значення Q _кр знаходяться в спеціальних таблицях.

Повернемося до нашого завдання. Введемо позначення: х – вибірка дівчат, y – вибірка юнаків. Для кожної вибірки будуємо ранжований ряд:

х: 28 30 34 34 35 36 37 39 40 41 42 42 43 44 45 46

y: 26 28 32 32 33 34 35 38 39 40 41 42 43 44

Підраховуємо число значень в областях ранжируваних рядів, які не перекриваються. В ряду х значення, які не перекриваються є 45 і 46, тобто N₁ = 2; в ряду y тільки 1 значення, яке не перекривається 26, тобто N₂ = 1. Звідси, Q = N₁ + N₂ = 1 + 2 = 3. У таблиці знаходимо, що Q _кр. = 7 (для рівня значущості р≤0,05) і Q _кр = 9 (для рівня значущості р≤0,01).

Висновок: оскільки Q < Q _кр, то за критерієм Розенбаума відмінності між вибірками не є статистично достовірними.

Примітка:

Критерій Розенбаума може використовуватися незалежно від характеру розподілу змінних, тобто в даному випадку відпадає необхідність використання критеріїв χ² Пірсона і λ Колмогорова для визначення типу розподілів в обох вибірках.

Дата добавления: 2014-10-15