Обмеження біноміального критерію

Біноміальний критерій m

На відміну від нормального і рівномірного розподілів, що описують поведінку змінної в досліджуваній вибірці випробуваних, біноміальний розподіл використовується для інших цілей. Він служить для прогнозування ймовірності двох взаємовиключних подій в деякому числі незалежних один від одного досліджень.

Критерій призначений для зіставлення частоти, що зустрічається якогось ефекту з теоретичною або заданою частотою, що зустрічається.

Застосовується у випадках, коли досліджена лише одна вибірка об’ємом не більше 300 спостережень, в деяких завданнях – не більше 50 спостережень.

Біноміальний критерій незамінний, якщо наявні 2 умови:

а) досліджена лише одна вибірка досліджуваних, і немає можливості ділити вибірку на дві частини з метою використання критерію φ⃰, так як досліднику важливо дослідити частоту, що зустрічається ознаки у вибірці в цілому;

б) в дослідженій вибірці менше 30 досліджуваних, що не дозволяє нам застосувати критерій χ².

Якщо в нашій вибірці більше 30 досліджуваних, ми можемо використовувати критерій m і тим самим економити час на підрахунок χ².

Якщо m_емп рівне або перевершує m_кр, то відмінності достовірні.

1. У вибірці повинно бути не менше 5 спостережень. Можливе застосування критерію і при 2≤n˂5, але тільки у відношенні відповідного типу завдань (Табл. XV).

2. Верхня межа чисельності вибірки варіює в діапазоні від 50 до 300 спостережень, що визначається таблицями критичних значень.

3. Біноміальний критерій m дозволяє перевірити лише гіпотезу про те, що частота зустрічання ефекту, який цікавить в досліджуваній вибірці переважає задану вірогідність Р. Задана вірогідність при цьому повинна бути: Р≤0,50.

4. Якщо ми хочемо перевірити гіпотезу про те, що частота зустрічання ефекту, який нас цікавить достовірно нижче заданої вірогідності, то при Р=0,50 ми можемо зробити за допомогою відомого критерію знаків G, при Р˃0,50 ми повинні перетворити гіпотези в протилежні, а при Р˂0,50 прийдеться використовувати критерій χ².

Задані вірогідності	Н1·fемп достовірно вище fтеор	Н1·fемп достовірно нижче fтеор
Р˂0,50	А m для 2≤n≤50	Б χ^2 для n≥30
Р=0,50	В m для 5≤n≤300	Г G для 5≤n≤300
Р˃0,50	Д χ^2 для n≥30	Є m для 2≤n≤50

А) Якщо задана вірогідність Р˂0,50, а f_емп˃f_теор (наприклад, допустимий рівень браку – 15%, а в досліджуваній вибірці отримано значення 25%), то біноміальний критерій можливий для вибірки 2≤n≤50.

Б) Якщо задана вірогідність Р˂0,50, а f_емп˂f_теор (наприклад, допустимий рівень браку – 15%, а в досліджуваній вибірці отримано значення 5%), то біноміальний критерій неможливий і необхідно використовувати критерій χ².

В) Якщо задана вірогідність Р=0,50, а f_емп˃f_теор (наприклад, вірогідність вибору кожної із ріновірогідних альтернатив Р=0,50, а в досліджуваній вибірці одна з альтернатив вибирається частіше, ніж в половині випадків), то біноміальний критерій можливий для об’єму вибірки 5≤n≤300.

Г) Якщо задана вірогідність Р=0,50, а f_емп˂f_теор (наприклад, вірогідність вибору кожної із рівновірогідних альтернатив Р=0,50, а в досліджуваній вибірці одна з альтернатив спостерігається рідше, ніж в половині випадків), то замість біноміального критерію застосовується критерій знаків G, який є «дзеркальним відображенням» біноміального критерію при Р=0,50. Допустимий об’єм вибірки: 5 ≤ n ≤ 300.

Д) Якщо задана вірогідність Р ˃ 0,50, а f_емп˃f_теор (наприклад, середньо-статистичний процент рішення задачі – 80%, а в досліджуваній вибірці він складає 95%), то біноміальний критерій неможливий і потрібно застосовувати критерій χ².

Є) Якщо задана вірогідність Р ˃ 0,50, а f_емп˂f_теор (наприклад, середньо-статистичний процент рішення задачі – 80%, а в досліджуваній вибірці він складає 60%), то біноміальний критерій можливий при умові, що в якості «ефекту» ми будемо розглядати більш рідкісну подію – невдачу у вирішенні задачі, вірогідність якої Q=1 – Р=1 – 0,80=0,20 і процент зустрічання в даній вибірці: 100% – 75% = 25%. Ці перетворення фактично приведуть дане завдання до завдання, передбаченого п. А. Допустимий об’єм вибірки: 2≤n ≤50.

Приклад: в процесі тренінгу сенситивності в групі з 14 осіб виконувалась вправа «Психологічний прогноз». Всі учасники повинні були пильно вглядатися в одну і ту ж людину, яка сама виразила бажання біти дослідженою цієї вправи. Потім кожний з учасників задавав питання на яке можливі тільки два варіанти відповіді «Що в тебе переважає: відсторонене спостереження чи включена емпатія?» або «Продовжував би ти працювати чи ні, якби в тебе з’явилась матеріальна можливість не працювати?». Досліджуваний повинен був мовчки вислухати, а під час паузи учасники намагалися визначити, яку він дасть відповідь на поставлене питання і записати свої прогнози. Потім ведучий пропонував досліджуваному дати відповідь на задане питання. Після того, як було задано 14 питань (13 учасників + ведучий), кожний повідомив, скільки у нього вийшло точних прогнозів. В середньому було по 7,8 співпадань, але в одного з учасників їх було 12, і група спонтанно йому зааплодувала. У іншого учасника, виявилося всього 4 співпадання, і він був засмученим.

Чи мала група статичне підґрунтя для аплодисментів?

Чи засмучений учасник мав привід для смутку?

Група матиме статистичні засади для аплодисментів, якщо частота правильних прогнозів у учасника А перевищить теоретичну частоту випадкових вгадувань. Відповідно до теорії вірогідності, шанси випадково вгадати або не вгадати відповідь становить Р=Q=0,5.

Визначимо теоретичну частоту правильних випадкових вгадувань:

f_теор = n ·P,

де n – кількість прогнозів;

Р – вірогідність правильного прогнозу при випадковому вгадуванні.

f_теор = 14·0,5=7,

Отже нам потрібно визначити, чи «переважують» 12 правильно даних прогнози 7 правильних прогнозів, які могли бути у даного учасника, якби він прогнозував відповідь досліджуваного випадковим чином.

Вимоги, передбачені обмеженням 3, дотримані: Р=0,50; f_емп˃f_теор. Даний випадок відноситься до «В».

Можемо сформулювати гіпотези.

Н₀: Кількість точних прогнозів в учасника А не перевищує частоту, яка відповідає вірогідності випадкового вгадування.

Н₁: Кількість точних прогнозів в учасника А перевищує частоту, яка відповідає вірогідності випадкового вгадування.

За Табл. ХІV визначаємо критичні значення критерію m при n=14, Р=0,50:

m_кр = 11 (р≤0,05)

12 (р≤0,01)

Емпіричне значення критерію m приймає емпірична частота:

m_емп = f _емп = 12

m_емп ≥ m_кр

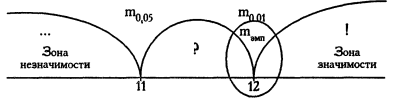
Висновок: Н₀ відхиляється. Кількість точних прогнозів у учасника А перевищує (рівне) критичній частоті вірогідності випадкового вгадування.

Друге завдання, визначити чи 4 точних прогнози учасника Б – це достовірно менше, ніж 7 теоретично можливих правильних прогнози при випадковому вгадуванні?

В даному випадку Р=0,50; f_емп˂f_теор У відповідності з обмеженням 4, в даному випадку ми повинні використати критерій знаків, який є дзеркальним відображенням або «другою стороною» біноміального критерію (варіант «Г»).

Спочатку потрібно визначити, що є типовою подією для учасника Б. Це неправильні прогнози їх 10. Тепер ми визначаємо, чи достатньо мало у нього нетипових правильних прогнозів, щоб вважати переважання неправильних прогнозів достовірними.

Формулюємо гіпотезу.

Н₀: Переважання неправильних прогнозів в учасника Б є випадковим.

Н₁: Переважання неправильних прогнозів в учасника Б не є випадковим.

За Табл. V визначаємо критичні значення критерію знаків G для n=14.

G_кр = 3 (р≤0,05)

2 (р≤0,01)

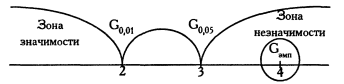
Емпіричне значення критерію G визначається як кількість нетипових подій. В даному випадку:

G_емп = 4

G_емп ˃ G_кр

Висновок: Н₀ приймається. Переважання неправильних прогнозів в учасника Б є випадковим. Учасник Б не мав достатніх статистичних засад для суму.

Класичний приклад біноміального розподілу – підкидання монети, яка падає на тверду поверхню. Рівноймовірні два результати (події): 1) монета падає «орлом» (ймовірність дорівнює р) або 2) монета падає «решкою» (ймовірність дорівнює q). Якщо третього результату не дано, то p = q = 0,5 і p + q = 1. Використовуючи формулу біноміального розподілу, можна визначити, наприклад, яка ймовірність того, що в 50 випробуваннях (число підкидань монети) остання випаде «орлом», припустимо, 25 разів.

Для подальших міркувань введемо загальноприйняті позначення:

n – загальне число спостережень;

i – число подій, які нас цікавлять (результатів);

n – i – число альтернативних подій;

p – емпірично визначена (іноді - передбачувана) ймовірність, яка цікавить нас;

q – ймовірність альтернативного події;

P_n (i) – прогнозована ймовірність цікавить нас i по певному числу спостережень n.

Формула біноміального розподілу:

У разі рівновірогідного результату подій (p = q) можна використовувати спрощену формулу:

Розглянемо приклади, що ілюструють використання формул біноміального розподілу в психологічних дослідженнях.

Приклад:

Припустимо, 5 студентів виконують інтелектуальний тест підвищеної складності. Правильне виконання тесту «+», неправильне «–». Кожен студент може мати 2 можливих результати (+ чи –), причому ймовірність кожного з цих фіналів дорівнює 0,5.

Студенти
Можливі результати	+ –	+ –	+ –	+ –	+ –

Необхідно визначити ймовірність того, що троє з 5 студентів успішно впораються з цим завданням.

Рішення

Всього можливих результатів: 2⁵ = 32.

Загальна кількість варіантів 3 (+) і 2 (–) становить

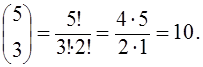
Лекція 11-13

Дата добавления: 2014-10-15