Непараметричні міри впливу

G – критерій знаків (Мак-Немара)

Критерій знаків використовується в тих випадках, коли вимір психологічної ознаки проводиться на одній і тій же групі (вибірці) досліджуваних до і після одноразового впливу фактора, який нас цікавить. Він дозволяє встановити, в яку сторону у вибірці в цілому змінюються значення ознаки при переході від першого виміру до другого: чи змінюються показники в сторону підвищення або підсилення, чи навпаки в сторону зниження або послаблення. Критерій знаків застосовується як до зсувів, які можна визначити лише якісно (наприклад, зміни негативного відношення на позитивне), так і до тих зсувів, які можуть бути виміряні кількісно (наприклад, скорочення часу роботи над завданням після експериментального впливу). Критерій знаків досить простий для обчислення і передбачає лише встановлення знака відмінностей між парами порівнюваних величин досліджуваної ознаки до і після впливу. Підсумовуючи число позитивних і негативних зрушень, знаходиться їх співвідношення і порівнюється з табличним (критичним). Вплив фактору вважається статистично достовірним, якщо відмінності значень перевищують табличне значення. Якщо в експериментальних даних є нульові зрушення (тобто досліджувана ознака не змінюється під впливом фактора), то такі результати виключаються з розгляду, а кількість спостережень n зменшується на число нульових зрушень.

Зсуви, які є переважаючими, називаються типовими, а зсуви незначні, одиничні, протилежні – нетиповими. Суть критерію знаків полягає в тому, що він визначає чи можна вважати кількість «типових» зсувів переважаючими. Отже, чим менше «нетипових зсувів», тим більша вірогідність вважати «типові зсуви» переважаючими. Чим менше G_емп, тим більш вірогідно, що зсув в «типовому» напрямку статистично достовірний.

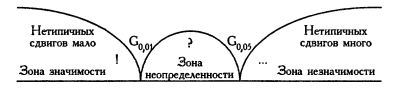
Графічне представлення позитивних і негативних зсувів.

В таблиці критерію знаків для різних n знаходиться критичне значення та порівнюється з емпіричним. Оскільки критерій знаків є одним з трьох виключень з загальних правил,то зона значимості простирається вліво, в сторону більш низьких значень і свідчіть про більшу достовірність «типових» зсувів.

Обмеження критерію знаків:

Кількість спостережень в обох вимірах повинна бути не менше 5 та не більше 300.

Приклад: Визначити, чи є зміна рівня тривожності статистично значущою. Результати вимірювання рівня тривожності до і після проведення тренінгу в групі випробуваних відображені в таблиці.

H₀: переважання типового напрямки зсуву є випадковим.

Н₁: переважання типового напрямки зсуву не є випадковим.

№ досліджуваних	Рівень тривожності «до» тренінгу	Рівень тривожності «після» тренінгу	Зсув
			+4
			–9
			–1
			–6
			+5
			+3
			+1
			+1
			+1
			–1
			–7
			+2
			+3

Для перевірки нульової гіпотези визначають типовий зсув ("+" або "–") і визначають число (кількість) типових і нетипових зсувів.

У прикладі число позитивних зсувів = 8 перевершує кількість зсувів у негативному напрямку = 5. Тому в даній задачі типовим є позитивне зрушення. З таблиці видно, що число n таких зрушень дорівнює 8.

Емпіричне значення критерію визначається, як число нетипових зрушень. У нашому випадку нетиповий негативний зсув G_емп = 5.

Критичне значення критерію Gкр (α;n) визначають за спеціальною таблицею, де n – загальне число зсувів, тобто обсяг вибірки. n = 13

G_кр = 3 (p≤0,05)

1 (p≤0,01)

Нульова гіпотеза приймається, якщо G_емп ≥ G_кр (α;n).

Оскільки G_емп = 5 > 3 = Gкр (0,05;13), то нульова гіпотеза приймається, і типовий напрямок зсуву є випадковим на обраному рівні значущості.

За відсутності відповідної таблиці, можна скористатися формулою наступного виду:

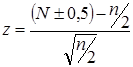
де N – сума плюсів чи сума мінусів, n – загальне число значень, 0,5 – поправочний коефіцієнт, який додають до N, якщо N < n/2, або віднімають, якщо N > n/2. Критичне значення z (міра Пірсона) для відповідного рівня значущості знаходиться у відповідних таблицях.

Дата добавления: 2014-10-15