T-критерій Стьюдента для залежних вибірок

Достовірності

Класифікація зсувів та критеріїв оцінки їх статистичної

Види зсувів	Об’єкт зіставлення	умови	Критерії оцінки достовірності зсуву
К-ть вимірів	К-ть груп
1. Часові, ситуаційні, мисленєві, вимірювальні	Одні й ті ж показники, виміряні у одних і тих же досліджуваних в різний час, в різних ситуаціях			G – критерій знаків Т – критерій Вілкоксона
3 і більше		L – критерій тенденцій Пейджа; χ^2r – критерій Фрідмана
2. Зсуви під впливом експериментальних впливів	Одні й ті ж показники, виміряні в одних і тих же досліджуваних до та після впливу: а) при відсутності контрольної групи			G – критерій знаків; Т – критерій Вілкоксона
3 і більше		L – критерій тенденцій Пейджа; χ^2r – критерій Фрідмана
б) за наявності контрольної групи			Варіант 1 – зіставлення значень «до» і «після» окремо за експер-ною та контрольною групами: G – критерій знаків; Т – критерій Вілкоксона Варіант 2 – зіставлення зсувів у двох групах: Q – критерій U – критерій Манна-Уїтні φ⃰ – критерій Фішера
3 і більше		Зіставлення значень окремо за експер-ною та контрольною групами: L – критерій тенденцій Пейджа; χ^2r – критерій Фрідмана
3. Структурні зсуви	Різні показники одних і тих же досліджуваних			G – критерій знаків; Т – критерій Вілкоксона
3 і більше		L – критерій тенденцій Пейджа; χ^2r – критерій Фрідмана

t-критерій був розроблений Вільямом Госсетом (1876-1937) для оцінки якості пива на пивоварних заводах Гіннесса в Дубліні (Ірландія). У зв'язку із зобов'язаннями перед компанією з нерозголошення комерційної таємниці (керівництво Гіннесса вважало таким використання статистичного апарату в своїй роботі), стаття Госсета вийшла в 1908 році в журналі «Біометрика» під псевдонімом «Student» (Студент).

Метод Стьюдента для залежних одна від одної вибірок (наприклад, для порівняння результатів, отриманих при повторному тестуванні на одній і тій же вибірці досліджуваних) використовують досить рідко, оскільки для цих цілей існують інші, більш інформативні статистичні прийоми. Проте, для даної мети в першому наближенні можна використовувати формулу Стьюдента такого вигляду:

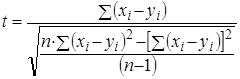
Отриманий результат порівнюють з табличним значенням для df = n –1 ступенів свободи, де n – число пар значень x і y. Результати порівняння інтерпретуються точно так само, як і у випадку обчислення відмінностей між двома незалежними вибірками.

d – середнє арифметичне різниць індивідуальних значень, S_d – стандартне відхилення значень різниць.

Кількість ступенів свободи

df = n – 1

Наступний приклад демонструє алгоритм розрахунку критерію.

Перед початком першого навчального року було виміряно рівень інтелекту у групи студентів. На початку другого навчального року за допомогою паралельної методики знову було виміряно рівень інтелекту. Оскільки можна використовувати результати тільки одних і тих же людей, з подальшої обробки були виключені результати тих студентів, які залишили навчання в інституті (що не піддалися обстеженню на фазі заключних зрізів). Чи можна сказати, що за рік навчання інтелектуальний рівень студентів значно змінився?

1. Формулюються статистичні гіпотези.

Н₀: зсув між показниками початкових і кінцевих зрізів недостовірний.

Н₁: зсув між показниками початкових і кінцевих зрізів достовірний.

2. Обчислюються значення t _емп і df.

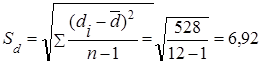
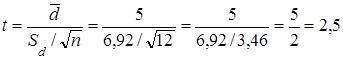
df = n –1 = 12–1=11

n	Початковий зріз (xi)	Кінцевий зріз (yi)	di = yi – xi	di – Md	(di – Md)^2
				–5
				–3
			–9	–14
				–2
			–4	–9
n=12		Ʃ di =60		Ʃ=528

t _кр (p≤0,05)=2,20

(p≤0,01)=3,11

Висновок: емпіричне значення перевищує критичне (при рівні значимості p <0,05 = 2,20), що говорить про наявність достовірних відмінностей між цими вибірками. Отже, нульова гіпотеза про відсутність відмінностей відхиляється.

Дата добавления: 2014-10-15