Т – критерій Вілкоксона

Аналогічно критерію знаків, критерій Т Вілкоксона використовується для зіставлення показників, виміряних в двох різних умовах на одній і тій же вибірці досліджуваних. Він дозволяє встановити не тільки спрямованість змін, але і їх вираженість, тобто визначає, чи є зрушення показників в якомусь одному напрямку більш інтенсивним, ніж в іншому. Критерій може бути використаний, якщо досліджувана ознака виміряна в шкалі порядку або шкалі інтервалів. Обсяг вибірки – від 5 до 50 осіб. Нульові зсуви з розгляду виключаються та кількість спостережень n зменшується на кількість цих нульових зсувів.

Пояснити алгоритм розрахунку можна на наступному прикладі. Припустимо, в кабіні літака (і на тренажері) змінили ергономічне середовище. Для виконання певного завдання льотчик раніше витрачав одну кількість секунд, а в новому середовищі він на виконання тих же дій витрачає іншу кількість часу. Таким чином, були зроблені виміри у 10 льотчиків. Визначити достовірність переважання зсуву значень в напрямку однієї зі сторін за умови, що результати другого зрізу обумовлені винятково зміною ергономічного середовища.

Формулюються статистичні гіпотези.

Н₀: переважання зсувів між початковими і кінцевими показниками в одному з напрямків недостовірні (значуще не відрізняються від нуля).

Н₁: переважання зсувів між початковими і кінцевими показниками в одному з напрямків достовірні (значимо відрізняються від нуля).

Визначаються величини зсувів між початковими і кінцевими показниками, потім вони переводяться в абсолютні значення і ранжуються за принципом «меншому значенню – менший ранг». Потім виділяються нетипові (чия спрямованість відрізняється від більшості) ранги і підраховується їх сума. Слід звернути увагу: у нашому прикладі одне із значень d дорівнює 0. Тому при ранжуванні різниць ми присвоюємо йому нульовий ранг.

n	Початкові показники	Підсумкові показники	Різниця показників (d)	Абсолютне значення	Ранг різниці
			–1
			+5		4,5
			–6		6,5
			+6		6,5
			–4		2,5
			–4		2,5
			–8
			–9
			+5		4,5

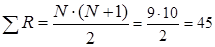
У таблиці нетипові ранги виділені жирним шрифтом. Сума нетипових рангів дорівнює емпіричному значенню.

T=Ʃ R_r

Де R_{r –} рангові значення зсувів з більш рідкісним знаком.

Т_емп = 4,5 + 6,5 + 4,5 = 15,5

За таблицею визначаємо значення Т для n=9

Т_кр = 8 (р≤ 0,05)

3 (р ≤0,01)

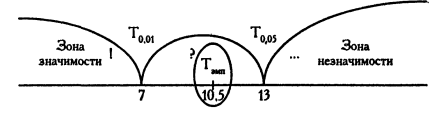
Для Т-критерію Вілкоксона, що представляє собою виключення із загального правила, принцип прийняття-відхилення нульової гіпотези є наступним: Т_емп < Т_кр => Н₁! Слід додатково додати, що цей критерій може бути одностороннім (якщо напрямок зсувів передбачується) і двостороннім (якщо ми не передбачаємо напрямок зсувів). Рівні значущості для одностороннього та двостороннього критеріїв різні. У нашому випадку ми маємо справу з двостороннім критерієм, бо попередньо не пророкували напрямок відмінностей.

Т_емп > Т_кр (р < 0,05) => Н₀! Ми можемо констатувати, що достовірність переважання зсувів ні в одному з напрямків не встановлена. Можливо, що ми могли б спростувати нульову гіпотезу, якби збільшили кількість спостережень.

Критерій χ_r² Фрідмана

Критерій χ_r² Фрідмана застосовується для співставлення показників, виміряних в трьох або більше умовах на одній і тій же вибірці досліджуваних.

Критерій дозволяє встановити, що величини показників від умови до умови змінюються, але при цьому не вказується напрямок змін.

Даний критерій є поширенням критерію Т Вілкоксона на більшу, ніж 2, кількість умов вимірів. Однак ми ранжуємо не абсолютні величини зсувів, а самі індивідуальні значення, отримані даним досліджуваним в 1,2,3 та наступним вимірах.

Після того, як всі значення будуть проранжовані, підраховуються суми рангів за стовбцями для кожного з проведених вимірів. Якщо відмінності між значеннями ознаки, які отримані в різних умовах, випадкові, то суми рангів за різними умовами будуть приблизно рівні. Але якщо значення ознаки змінюються в різних умовах якимсь закономірним чином, то в одних умовах будуть переважати високі ранги, а в інших – низькі. Суми рангів будуть достовірно відрізнятися між собою. Емпіричне значення критерію χ_r² і вказує на те, наскільки відрізняються суми рангів. Чим більше емпіричне значення χ_r², тим більш суттєві відмінності суми рангів воно відображає.

Якщо χ_r² дорівнює критичному значенню або перебільшує його, відмінності статистично достовірні.

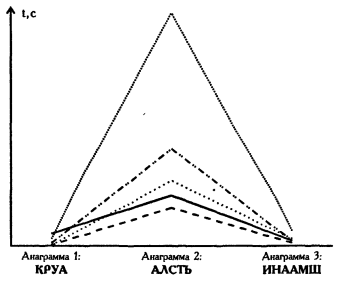
Графіки змін часу вирішення трьох анаграм у п’яти досліджуваних.

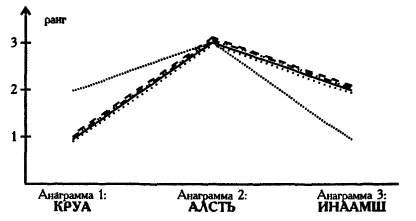
Графіки змін ранжованих показників часу вирішення анаграм.

Обмеження критерію:

1. Нижній порог: не менше 2-х досліджуваних (n≥2), кожний з яких пройшов не менше 3-х вимірів (с≥3).

2. При с=3, n≤9, рівень значимості отриманого емпіричного значення χ_r² визначається за таблицею χ_r² Фрідмана (Табл.VII-А); при с=4, n≤4, рівень значимості отриманого емпіричного значення χ_r² визначається за таблицею (Табл. VII-Б); при більших кількостях досліджених або умов отримані емпіричні значення χ_r² зіставляються з критичними значеннями χ², які визначаються за таблицею (Табл. ІХ). це пояснюється тим, що χ_r² має розподіл, схожий з розподілом χ². Число ступенів свободи df визначається за формулою:

df = c – 1

де с – кількість умов вимірів

Приклад: в експерименті з дослідження інтелектуальної наполегливості досліджувані вирішували анаграми, які ускладнювались і вимагали більшого часу на розв’язання. Чи достовірні відмінності у часі вирішення досліджуваними анаграм?

Н₀: відмінності в часі, який досліджувані проводять над вирішенням трьох різних анаграм, є випадкові.

Н₁: відмінності в часі, який досліджувані проводять над вирішенням трьох різних анаграм, не є випадковими.

Код імені досліджуваного	Анаграма 1: КРУА (РУКА)	Анаграма 2: АЛСТЬ (СТАЛЬ)	Анаграма 3: ИНААМШ (МАШИНА)
1. Л-в
2. П-о
3. К-в
4. Ю-ч
5. Р-о
Суми
Середні	10,2		248,8		9,4

Загальна сума рангів R=6+15+9=30

Розрахункова формула рангів:

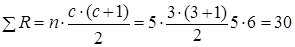
Де n – кількість досліджуваних;

с – кількість умов вимірів.

Визначаємо емпіричне значення χ_r² за формулою:

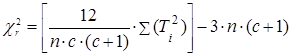
Де с – кількість умов;

n – кількість досліджуваних;

T_i – суми рангів за кожною умовою.

Визначаємоχ_r² для даного випадку:

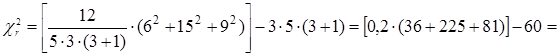
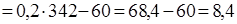
Оскільки в даному прикладі розглядаються три завдання, тобто 3 умови, с =3. Кількість досліджуваних n=5. Це дозволяє нам скористатися спеціальною таблицею χ_r² (Табл. VII-A)

Емпіричне значення χ_r²=8,4 при с=3, n=5 точно відповідає рівню значимості р =0,0085.

Висновок: Н₀ відхиляється. Відмінності в часі, який досліджувані проводять над вирішенням трьох різних анаграм, невипадкові (р=0,0085).

Дата добавления: 2014-10-15