U-критерій Манна-Уїтні

Непараметричний U- критерій Манна-Уїтні дозволяє оцінити достовірність відмінностей у незалежних вибірках, якщо дані в них представлені в ранговій шкалі. Цей критерій слід застосовувати і в тому випадку, якщо дані представлені в метричних шкалах, але не вкладаються в криву нормального розподілу. При цьому слід звернути на обмеження у використанні критерію: у кожній вибірці має бути не менше трьох і не більше 60 спостережень.

Обидві вибірки об'єднуються, здійснюється ранжування за принципом «меншому значенню – менший ранг», потім об'єднана вибірка знову розщеплюється, але зі збереженням значень рангів, присвоєних при об'єднаному ранжируванні.

Як приклад пропонується проаналізувати 20 значень з таблиці з метою з'ясувати, чи існують для хлопчиків і дівчаток достовірні відмінності між результатами субтестів на обізнаність.

Формулюються статистичні гіпотези.

Н₀: різниця між показниками субтеста обізнаності у хлопчиків і дівчаток статистично не достовірна.

Н₁: різниця між показниками субтеста обізнаності у хлопчиків і дівчаток статистично достовірна.

ж

ж

ч

ж

ж

ж

ч

ж

ж

ж

ж

ч

ж

ж

ч

ж

ч

ж

ч

ч

ж

ж

ч

ч

ж

ж

ч

ч

ж

ж

ч

ж

ч

ж

ж

ж

ж

ч

ж

ж

3,5

3,5

5,5

5,5

7,5

7,5

12,5

12,5

Порахувати рангові суми

Обізнаність ч	Ранг	Обізнаність ж	Ранг
	3,5
	3,5
			5,5
			5,5
	7,5
	7,5
	12,5
			12,5
	Ʃr=60,5		Ʃr=149,5

Загальна сума рангів: 60,5+149,5=210. Розрахункова сума:

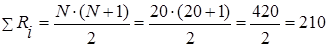
Визначається емпіричне значення критерію за формулою:

де n₁ – об’єм першої вибірки;

n₂ – об’єм другої вибірки;

Т_х – більша з рангових сум;

n_х – об’єм групи з більшою сумою рангів.

Згідно з таблицями критичних значень, при n ₁=13 і n ₂=7,

U_кp (для р <0,05) = 20 і

U_кр (для р <0,01) = 13.

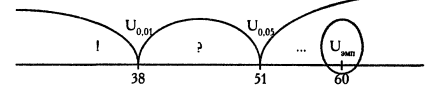
Критерій Манна-Уїтні відрізняється від більшості інших критеріїв тим, що для спростування нульової гіпотези емпіричне значення повинно бути менше або дорівнює критичного (подібна закономірність типова також для Т -критерію Вілкоксона і критерію знаків G). Тобто використовується наступний принцип: U _емп ≤ U _кp = ˃ Н₁!

У нашому випадку U _емп = 32,5. Тобто U _емп > U _кp (р <0,05)=>Н₀! Таким чином, наявність достовірних відмінностей між показниками обізнаності у хлопчиків і у дівчаток не встановлено. Якщо необхідно порівняти не два, а більшу кількість розподілів, то в цьому випадку використовується Н -критерій Краскела-Уоллеса.

Н -критерій Краскела-Уоллеса (Kruskal-Wallis)

Н -критерій Краскела-Уоллеса призначається для оцінки відмінностей за будь-яким показником між трьома і більше вибірками. Обмеження у використанні критерію наступне: у кожній з вибірок має бути не менше трьох спостережень (якщо всього два спостереження, то слід застосувати U -критерій).

Як і у випадку з U -критерієм, вибірки об'єднуються, ранжуються за принципом «меншому значенню – менший ранг», потім об'єднана вибірка знову розщеплюється, але значення рангів присвоєних при об'єднаному ранжируванні зберігаються.

Формула критерію виглядає наступним чином:

де R – це суми рангів по групах; k – кількість груп; n_k – об’єм груп; n – об’єм об'єднаної вибірки.

де Т – це суми рангів по кожній групі; N – загальна кількість досліджуваних в об’єднаній вибірці; n – кількість досліджуваних в кожній групі.

У разі, коли у нас k ≥ 4, для визначення критичного показника використовується таблиця критичних значень «хі -квадрат», так як при кількості груп більше трьох розподіл H -критерію наближається до розподілу χ². Якщо k = 3, то слід або взагалі застосувати U -критерій для попарного порівняння, або використовувати таблицю представлену в підручнику Е. В. Сидоренко. Автор публікує таблицю критичних значень H -критерію стосовно до k = 3, містить для кожної комбінації об’ємів груп до 6 градацій рівня значущості.

Ступінь свободи Н -критерію має формулу: df = k – 1.

Постановка завдання: необхідно з'ясувати, чи є достовірні відмінності в ступені стресостійкості у представників чотирьох груп студентів. У педагогічному вузі протестували студентів чотирьох різних факультетів старших курсів навчання за допомогою «Методики визначення стресостійкості та соціальної адаптації» Холмса-Раге. Дані зведені в таблицю.

№	Факультет	Тестові бали
	Психолого-педагогічний
	Психолого-педагогічний
	Психолого-педагогічний
	Фізики
	Фізики
	Фізичної культури
	Фізичної культури
	Фізичної культури
	Фізичної культури
	Фізичної культури
	Музики
	Музики
	Музики

Наступний етап – ранжування цієї об'єднаної вибірки і її розщеплення на чотири групи.

Фізичної культури	Фізики	Психолого-педагогічний	музики
Бал	Ранг	Бал	Ранг	Бал	Ранг	Бал	Ранг
							7,5
					7,5
	Ʃr1=15		Ʃr2=15		Ʃr3=29,5		Ʃr4=31,5

Загальна сума рангів = 15+15+29,5+31,5 = 91. Розрахункова сума рангів

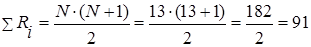
Обчислюються також об’єми груп:

n₁ = 5,

n₂ = 2,

n₃ = 3,

n₄ = 3.

Їх сума говорить про загальну кількість обстежених n = 13.

Потім обчислюється емпіричне значення критерію і ступеню свободи:

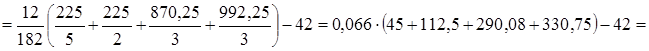
df = k –1 = 4–1 =3

Оскільки k=4, для визначення критичного значення критерію використовуємо таблицю розподілу статистики χ².

χ²_кр (р≤0,05) = 7,815

(р≤0,01) = 11,345

Н _емп = 9,4;

Н _кр (для р <0,05) = 7,815;

Н _емп > Н _кр (р <0,05)=˃Н₁! Таким чином, на рівні статистичної значущості встановлено наявність достовірних відмінностей між показниками стресостійкості у студентів різних факультетів.

Дата добавления: 2014-10-15