Дифференцируемость и полный дифференциал функции

Пусть функция определена в некоторой окрестности точки . Составим полное приращение функции в точке :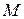

.

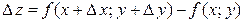Определение 1.8. Функция называется дифференцируемой в точке , если ее полное приращение в этой точке можно представить в виде

, (1.1)

где и при . Сумма первых двух слагаемых в равенстве (1.1) представляет собой главную часть приращения функции.

Определение 1.9. Главная часть приращения функции , линейная относительно и , называется полным дифференциалом этой функции и обозначается символом :

. (1.2)

Выражения и называются частными дифференциалами. Для независимых переменных 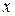и 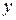полагают и 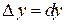. Поэтому равенство (1.2) можно представить в виде

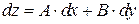. (1.3)

Надо отметить, если функция дифференцируема в точке , то она непрерывна в этой точке, имеет в ней частные производные и 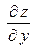, причем , . Тогда формула для вычисления полного дифференциала примет вид:

. (1.4)

Для функции 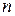переменных полный дифференциал определяется выражением

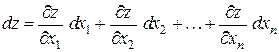. (1.5)

Пример 1.4. Найти полный дифференциал функции .

Решение. Находим частные производные первого порядка:

, , .

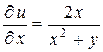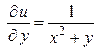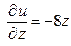Согласно формуле (1.5) получаем

.

,

Полный дифференциал функции (формула (1.4)) называется также дифференциалом первого порядка.

Введем понятие дифференциала высшего порядка. Пусть функция имеет непрерывные частные производные второго порядка. Дифференциал второго порядка определяется по формуле и имеет следующий вид:

. (1.6)

Аналогично можно получить формулы для дифференциала третьего и более высокого порядков.

Пример 1.5. Найти 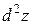, если .

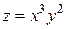Решение. Находим частные производные первого порядка:

.

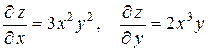Находим частные производные второго порядка:

, , .

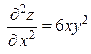Согласно формуле (19.6) получаем

.

,

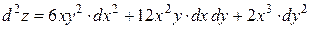2. ИСПОЛЬЗОВАНИЕ ЧАСТНЫХ ПРОИЗВОДНЫХ

В ИССЛЕДОВАНИИ ФНП

Дата добавления: 2014-10-15