
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Противоположные события
|
|
|
|
События. Равенство событий. Сумма и произведение событий.
Тема №1
Событием называется результат некоторого опыта.
Событие называется случайным, если в данном опыте оно может наступить, но может и не наступить.
Случайные события обозначаем А, В, С,…
Событие называется достоверным, если в данном опыте оно обязательно наступит. Достоверное событие обозначаем U. Событие называется невозможным, если в данном опыте оно наступить не может. Невозможное событие обозначаем V.
Событие А называется частным случаем события В, если при наступлении А наступает и В. То, что А является частным случаем В, записываем А Ì В.
События А и В называются равными, если каждое из них является частным случаем другого. Равенство событий А и В записываем А = В.
Суммой событий А и В называется третье событие А + В, которое наступает тогда и только тогда, когда наступает хотя бы одно из событий: А или В.
Произведением событий А и В называется третье событие АВ, которое наступает тогда и только тогда, когда оба события: А и В.
Понятия суммы и произведения двух событий очевидным образом переносятся на случай любого множества событий.
Событием, противоположным событию А, называется событие 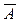 , которое наступает тогда и только тогда, когда не наступает событие А.
, которое наступает тогда и только тогда, когда не наступает событие А.
Условившись обозначать наступление события цифрой «1» и ненаступление – цифрой «0», сумму и произведение двух событий, а также противоположное событие можно определить следующими таблицами:
| А | В | А+В | АВ | А | 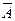
| |
Пример 1. Опыт состоит в бросании игральной кости. Событие Аi, (i = 1, 2, 3, 4, 5, 6) – выпадение i очков; событие А – выпадение четного числа очков, В – выпадение нечетного числа очков, С – выпадение числа очков, кратного трем, и D – выпадение числа очков, большего трех. Выразите события А, В, С и D через Аi, (i = 1, 2, 3, 4, 5, 6).
Решение. Событие А наступает тогда и только тогда, когда наступает А2, или А4, или А6. Это означает, что А = А2 + А4 + А6.
Рассуждая аналогично, имеем:
В = А1 + А3 + А5, С = А3 + А6 и D = А4 + А5 + А6.
Пример 2. С помощью таблиц, определяющих А + В, АВ и 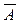 , доказать равенство А +
, доказать равенство А + 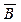 = А +
= А + 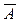
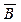 .
.
Решение. Составим таблицы, дающие все случаи наступления и ненаступления левой и правой частей доказываемого равенства:
| А | В | 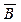
| А+ 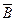
| А | В | 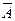
| 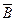
| 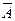 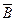
| А+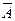 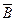
| |
Последние столбцы этих таблиц одинаковы, что и означает справедливость равенства А + 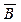 = А +
= А + 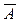
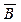 .
.
Пример 3. С помощью таблицы перечислите все случаи наступления и ненаступления события А 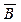 + С в зависимости от наступления и ненаступления событий А, В и С.
+ С в зависимости от наступления и ненаступления событий А, В и С.
Решение. Составим таблицу:
| А | В | С | 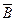
| А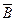
| А + С + С
|
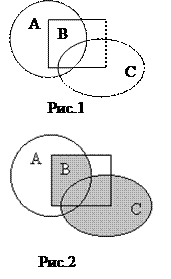 |
Пример 4. Пусть А, В и С – события, означающие попадание точки соответственно в области А, В и С (рис.1). Что означает событие АВ + С?
Решение. События АВ + С означает попадание точки в область (А Ç В) È С, которая на рисунке 2 заштрихована.
Контрольное задание №1
1. Опыт состоит в том, что стрелок произвел 3 выстрела по мишени. Событие Аi – попадание в мишень при i-м выстреле (i = 1, 2,3). Выразите через А1, А2 и А3 следующие события:
А – хотя бы одно попадание,
В – три промаха,
С – три попадания,
D – хотя бы один промах,
Е – не меньше двух попаданий,
F – не больше одного попадания,
G – попадание в мишень после первого выстрела.
2. Опыт состоит в бросании трех монет. Пусть монеты занумерованы и события Г1, Г2 и Г3 означают выпадение герба соответственно на первой, второй и третьей монетах. Выразите через Г1, Г2 и Г3 следующие события:
А – выпадение одного герба и двух цифр,
В – выпадение не более одного герба,
С – число выпавших гербов меньше числа выпавших цифр,
D – выпадение хотя бы двух гербов,
Е – на первой монете выпал герб, а на остальных – цифры,
F – на первой монете выпала цифра и хотя бы на одной из остальных выпал герб.
3. Пусть А, В и С – произвольные события. Что означают следующие события:  ВС,
ВС, 
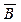
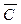 ,
, 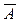 +
+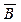 +
+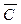 , А
, А 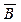
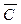 +
+ 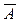 В
В 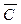 +
+ 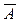
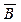 С,
С, 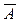
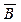
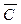 +
+ 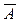
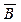 С +
С + 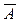 В
В 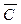 + А
+ А 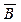
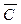 ?
?
4. Прибор состоит из 2 блоков I типа и 3 блоков II типа. Событие Ak (k = 1,2) – исправен k-й блок I типа; Bi (i = 1, 2, 3) – исправен i-й блок II типа.
Прибор работает, если исправен хотя бы один блок I типа и не менее 2 блоков II типа. Выразите событие С, означающее работу прибора, через Ak и Bi.
5. Судно имеет одно рулевое устройство, 4 котла и 2 турбины. Событие А означает исправность рулевого устройства, Вk (k = 1, 2, 3, 4) – исправность k-го котла и Сi (i = 1,2) – исправность i-й турбины; событие D – судно управляемое, что будет, когда исправны рулевое устройство, хотя бы один котел и хотя бы одна турбина. Выразите D и 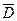 через А, Вk и Сi.
через А, Вk и Сi.
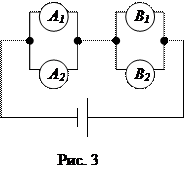
6. Электрическая цепь составленная по схеме, приведенной на рисунке 3.
Выход из строя элемента Ak (k = 1,2) событие Ak, элемента Bi (i = 1,2) событие Bi.
Запишите события С и 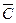 , если С означает разрыв цепи.
, если С означает разрыв цепи.
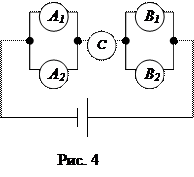
7. Электрическая цепь составлена по схеме, приведенной на рисунке 4. Выход из строя элемента Ak (k = 1,2) событие Ak, Элемента С – событие С и элемента Bi (i = 1,2) событие Bi.Запишите события D и 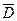 , если D – разрыв цепи. Электрическая цепь составлена по схеме, приведенной на рисунке 5.
, если D – разрыв цепи. Электрическая цепь составлена по схеме, приведенной на рисунке 5.
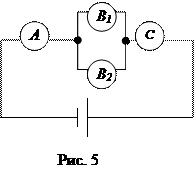
Выход из строя элемента А – событие А, элемента Bk (i = 1,2) – событие Bk и элемента С – событие С.Запишите события D и 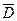 , если D – разрыв цепи.
, если D – разрыв цепи.
9. Производятся наблюдения за группой, состоящей из четырех однородных объектов. Каждый из них за время наблюдения может быть обнаружен или не обнаружен. Рассматриваются события:
А – обнаружен ровно один из 4 объектов;
В – обнаружен хотя бы один из объектов;
С – обнаружено не менее 2 объектов;
D – обнаружено ровно 2 объекта;
Е – обнаружено ровно 3 объекта;
F – обнаружены все 4 объекта.
Укажите, в чем состоят события:
1) А + В; 2) АВ; 3) В + С; 4) ВС; 5)
10. Опыт состоит в бросании точки в прямоугольник. События А, В и С означают соответственно попадание точки в области А, В и С (рис.6). Что означают следующие события:
а) А + В + С; б) АВС; в) 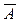 +
+ 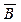 +
+ 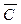 ;
;
г) 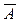 +
+ 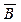 + С; д) А + В +
+ С; д) А + В + 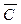 ; е) АВ +
; е) АВ + 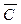 ; ж) АВ
; ж) АВ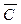 ; з) А
; з) А 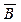 + С?
+ С?
|
|
|
|
|
Дата добавления: 2014-10-22; Просмотров: 1650; Нарушение авторских прав?; Мы поможем в написании вашей работы!