Тема №3

Классический способ подсчета вероятностей

Пусть W - конечное пространство элементарных событий А₁, А₂, …, А_n. В качестве борелевского поля событий рассмотрим систему S всех подмножеств множества W.

Ясно, что при этом аксиомы I и II выполняются. При классическом способе подсчета вероятностей все элементарные события считаются равновероятными. И так как р(А₁ + А₂ +… + А_n) = р(U) = 1, то р(А₁) = р(А₂) = … = р(А_n) = .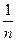

Если теперь А – произвольное событие и А = A_i1 + …+ A_im, то согласно аксиоме 2 имеем р(А) = .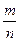

События А₁, А₂, …, А_n принято называть элементарными исходами данного испытания, а те элементарные исходы, которые в сумме составляют событие А, называются благоприятными случаями для А. Количество благоприятных случаев для события А обозначим m(A). Таким образом, р(А) = 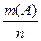, т.е. вероятность события А равна отношению числа благоприятных случаев для А к общему числу элементарных исходов испытания.

Пример 1. В урне 10 шаров, из которых 3 белых и 7 черных. Какова вероятность того, что наудачу извлеченный шар из этой урны окажется белым?

Решение. Пусть событие А – извлеченный шар оказывается белым. Данное испытание имеет 10 равновероятных исходов, из которых для события А благоприятны три. Следовательно, р(А) = .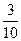

Пример 2. Все натуральные числа от 1 до 20 записаны на одинаковых карточках и помещены в урну. После тщательного перемешивания карточек из урны наудачу взята одна карточка. Какова вероятность того, что число на взятой карточке окажется кратным 5 – событие А; кратным 3 – событие В; простым – событие С; составным – событие D; не простым и не составным – событие Е?

Решение. Испытание имеет 20 равновероятных исходов. Из них m(A) = 4; m(B) = 6; m(C) = 8; m(D) = 11; m(E) = 1.

Соответственно событиям получим следующие вероятности:

p(A) = 0,2; p(B) = 0,3; p(C) = 0,4; p(D) = 0,55; p(E) = 0,05.

Контрольное задание №3

1. Наудачу выбрано натуральное число, не превосходящее 20. Какова вероятность того, что это число кратно 5?

2. Наудачу выбрано натуральное число, не превосходящее 20. Какова вероятность того, что это число окажется делителем 20?

3. Наудачу выбрано двузначное число. Какова вероятность того, что это число окажется: а) простым; б) составным; в) кратным 5; г) взаимно простым с 100?

4. Наудачу выбрана кость домино из полного набора. Какова вероятность того, что сумма очков на выбранной кости равна 5?

5. На одинаковых карточках написаны в троичной системе счисления все целые числа от 1 до 15. Наудачу извлекается одна карточка. Какова вероятность того, что выбранное число в своей записи содержит: а) не менее 2 единиц; б) хотя бы одну двойку; в) один нуль?

6. В урне a белых и b черных шаров. Какова вероятность того, что наудачу извлеченный шар из этой урны окажется белым?

7. В урне a белых и b черных шаров. Из этой урны вынимают один шар и откладывают в сторону. Этот шар оказался белым. После этого из урны берут еще один шар. Какова вероятность того, что этот шар также белый?

8. Какова вероятность того, что в наудачу выбранном двузначном числе цифры одинаковы?

9. Наудачу выбрано натуральное число, не превосходящее 100. Какова вероятность того, что выбранное число при делении на 8 дает в остатке 2?

10. Наудачу выбрано двузначное число. Какова вероятность того, что выбранное число имеет простой делитель, больший 10?

Дата добавления: 2014-10-22