Правила сложения и умножения вероятностей

Тема №6

Во многих задачах сложные события, вероятности которых надо найти, удается выразить в виде комбинации других, более простых событий, причем вероятности последних либо заданы, либо непосредственно подсчитываются. В таком случае для решения задач можно использовать формулы, выражающие вероятности суммы и произведения событий через вероятности соответствующих слагаемых и сомножителей.

Правила сложения и умножения вероятностей: если события А₁, А₂,…,А_n, … попарно несовместны, то справедливо равенство

р(А₁+ А₂,+…+ А_n +…) = р(А₁) + р(А₂) +…+ р(А_n)+... (1)

Из правила сложения вероятностей для двух событий вытекает правило нахождения вероятности противоположного события:

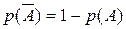. (2)

Для произвольных событий А и В имеет место формула (см. §3, задача 37(а)):

р(А + В) = р(А) + р(В) – р(АВ). (3)

В случае n слагаемых (n>2) эта формула принимает вид (см. §3, задача 38):

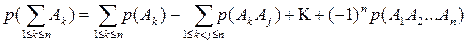. (4)

Вероятность р(В/А) события В при условии наступления события А по определению равна:

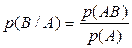. (5)

Из этого определения следует формула для вычисления вероятности произведения двух событий:

р(АВ) = р(А) р(В/А). (6)

Для вычисления вероятности произведения n событий (n>2) служит общая формула:

р(А₁ А₂… А_n) = р(А₁) р(А₂ / A₁) p(A₃ / A₁A₂)+…+ р(А_n /A₁A₂…A_n-1) (7)

События А₁, А₂,… А_n называются независимыми в совокупности, если вероятность любого из них не меняется при наступлении какого угодно числа событий из остальных.

Правило умножения вероятностей для n событий: если события А₁, А₂,… А_n независимы, то вероятность их произведения равна произведению их вероятностей, т.е.

р(А₁ А₂… А_n) = р(А₁) р(А₂) … р(А_n). (8)

Вычисление вероятности суммы событий можно свести к вычислению вероятности произведения противоположных событий по формуле

р(А₁ +А₂ +…+ А_n) = 1 - р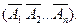 (9)

В частности, если события А₁,А₂,…, А_n независимы, то

р(А₁ +А₂ +…+ А_n) = 1 - р =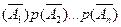

= 1 – (1 – р(А₁))(1 – р(А₂))…(1 – р(А_n)). (10)

Пример 1. Вероятность попадания в мишень для первого стрелка 0,8, а для второго – 0,6. Стрелки независимо друг от друга сделалают по одному выстрелу. Какова вероятность того, что в мишень попадет хотя бы один из стрелков?

Решение. Введем обозначения: событие А – попадание первого стрелка, событие В – попадание второго стрелка, событие С – попадание хотя бы одного из стрелков. Тогда, очевидно С = А + В, причем события А и В совместны. Следовательно, по формуле (3)

р(С) = р(А) + р)В) – р(АВ).

Так как события А и В независимы, то

р(С) = р(А) + р)В) – р(А) р(В).

Наконец, учитывая, что р(А) = 0,8, р(В) = 0,6, получаем:

р(С) = 0,8 + 0,6 – 0,8 · 0,6 = 0,92.

Пример 2. Монета брошена три раза. Найдите вероятность того, что герб выпадет ровно два раза.

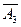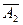Решение. Введем обозначения: А_i – выпадение герба при i-м бросании монеты (i = 1, 2, 3), А – выпадение 2 гербов при 3 бросаниях монеты. Тогда А = А₁А₂+ А₁А₃ + 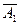А₂А₃. Так как слагаемые правой части этого равенства попарно несовместны, то по правилу сложения вероятностей имеем:

р(А) =р(А₁А₂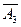) + р(А₁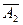А₃) + р(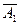А₂А₃).

Наконец, учитывая независимость событий А₁, А₂, А₃, по правилу умножения вероятностей получаем:

р(А) =р(А₁ ) р(А₂ ) р(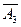) + р(А₁ ) р(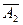) р(А₃) + р(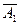) р(А₂ ) р(А₃)=

=.

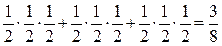Пример 3. В команде из 12 спортсменов 5 мастеров спорта. По жеребьевке из команды выбирают 3 спортсменов. Какова вероятность того, что все выбранные спортсмены являются мастерами спорта?

Решение. Укажем 2 способа решения, из которых первый состоит в непосредственном подсчете искомой вероятности по классической схеме, а второй – в применении формулы (7).

Первый способ. Представим себе урну, в которой 5 красных и 7 белых шаров. Красные шары соответствуют мастерам спорта, а белые – остальным спортсменам. Из этой урны наудачу извлекаются 3 шара, и пусть событие А состоит в появлении 3 красных шаров. Тогда искомая вероятность равна: .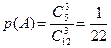

Второй способ. Из урны последовательно без возвращения извлекаются 3 шара. Введем обозначения: А₁ – первый шар красный, А₂ – второй красный, А₃ – третий красный и А – все 3 шара красные. Тогда А = А₁А₂А₃ и по формуле (7) при n = 3 имеем:

р(А) = р(А₁) р(А₂/A₁) p(A₃/A₁A₂) = .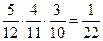

Пример 4. 3 стрелка попадают в мишень соответственно с вероятностями 0,9; 0,8; 0,7. Какова вероятность того, что при одном выстреле хотя бы один из них попадет в мишень (событие D)?

Пусть событие А, В, С – соответственно попадание в мишень 1, 2, и 3-го стрелка. Тогда D= А + В + С. Однако лучше представить D как событие, противоположное 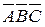(ни одного попадания): D = 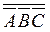. По формуле (10) тогда имеем: p(D) = 1 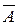– p(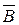) p() p(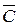) = 1 – 0,1 · 0,2 · 0,3 = 0,994.

Контрольное задание №6

1. 2 стрелка сделали по одному выстрелу по мишени. Известно, что вероятность попадания в мишень для одного из стрелков равна 0,6, а для другого – 0,7. Найдите вероятность того, что:

а) только один из стрелков попадет в мишень;

б) хотя бы один из стрелков попадет в мишень;

в) оба стрелка попадут в мишень;

г) ни один из стрелков не попадет в мишень;

д) ни один из стрелков не попадет в мишень.

2. Вероятность попадания в мишень при одном выстреле для первого стрелка равна р, а для второго – 0,7. Известно, что вероятность ровно одного попадания при одном выстреле обоих стрелков равна 0,38. Найдите р.

3. Вероятность того, что при одном измерении некоторой физической величины будет допущена ошибка, превышающая заданную точность, равна 0,2. Произведены 3 независимых измерения. Найдите вероятность того, что не более чем в одном измерении допущенная ошибка превысит заданную точность.

4. В ящике 10 деталей, среди которых 7 окрашенных. Сборщик наудачу достает 4 детали. Найдите вероятность того, что все взятые детали окрашенные.

5. Вероятность выигрыша по одному билету лотереи равна 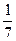. Какова вероятность, купив 5 билетов, выиграть: а) по всем пяти билетам; б) ни по одному билету; в) хотя бы по одному билету?

6. Детали проходят 3 операции обработки. Вероятность получения брака на первой операции равна 0,02; на второй – 0,03; на третьей – 0,02. Найдите вероятность получения детали без брака после 3 операций, предполагая, что получения брака на отдельных операциях являются независимыми событиями.

7. Из цифр 1, 2, 3, 4,5 выбирается одна, а из оставшихся – вторая. Найдите вероятность того, что будет выбрана нечетная цифра: а) первый раз; б) второй раз; в) оба раза.

8. Вероятность хотя бы одного попадания в цель при 4 независимых выстрелах равна 0,9984. Найдите вероятность попадания при одном выстреле.

9. Среди облигаций займа половина выигрышных. Сколько облигаций надо взять, чтобы быть уверенным в выигрыше хотя бы на одну облигацию с вероятностью, большей 0,95?

10. Абонент забыл последнюю цифру номера телефона и поэтому набирает ее наудачу. Найдите вероятность того, что ему придется сделать не более чем 2 неудачные попытки.

Дата добавления: 2014-10-22