Приближенные формулы Лапласа и Пуассона

Тема №9

Локальная приближенная формула Лапласа. При больших n имеет место приближенное равенство

, (1)

где , .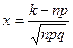

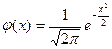(Таблицу значений функции j(х) см. в приложении).

Интегральная приближенная формула Лапласа. При больших n имеет место приближенное равенство

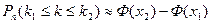, (2)

где

, , .

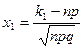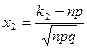Функция Ф (х) называется функцией Лапласа (таблицу ее значений см. в приложении). При нахождении значений функции j(х) и Ф (х) для отрицательных значений аргументов следует иметь в виду, что j(х) четная, а Ф (х) – нечетная.

Отметим еще, что приближенными формулами Лапласа (1) и (2) на практике пользуются в случае, если npq ³ 10. Если же npq < 10, то эти формулы приводят к довольно большим погрешностям.

Приближенная формула Пуассона. При больших n и малых р справедлива формула

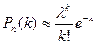, где l = np. (3)

(Для функции таблицу значений см. в приложении).

Пример 1. Вероятность наступления события А в каждом из 900 независимых испытаний равна р = 0,8. Найдите вероятность того, что событие А произойдет: а) 750 раз; б) 710 раз; в) от 710 до 740 раз.

Решение: Так как npq = 900 × 0,8 × 0,2 = 14,4 > 10, то в пунктах а) и б) воспользуемся формулой (1), а в пункте в) – формулой (2).

а) 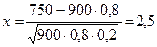; j(2,5)» 0,0175;

Р₉₀₀ (750)» ;

б) 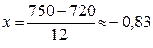; j (- 0,83) = j (0,83)» 0,2827;

Р₉₀₀ (710)» ;

в) ; ;

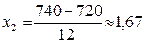Ф(-0,83) = - Ф(0,83)» - 0,2967; Ф(1,67)» 0,4527;

Р₉₀₀ (710 £ k £ 740)» 0,4525 + 0,2967 = 0,7492.

Пример 2. Вероятность того, что электролампочка, изготовленная данным заводом, является бракованной, равна 0,02. Для контроля отобрано наудачу 1000 лампочек. Оцените вероятность того, что частота бракованных лампочек в выборке отличается от вероятности 0,02 менее чем на 0,01.

Решение. Пусть k – число бракованных лампочек в выборке. Нам нужно оценить вероятность выполнения неравенства

.

Оно равносильно неравенству 11 £ k £ 29. Следовательно

.

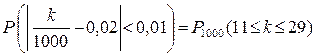Так как npq = 1000 × 0,02 × 0,98 = 19,6 > 10, то для вычисления вероятности Р₁₀₀₀ (11 £ k £ 29) воспользуемся интегральной приближенной формулой Лапласа. В данном случае

; ;

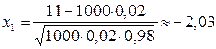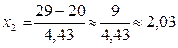Ф(- 2,03)» - 0, 4788; Ф(2,03)» 0,4788.

Следовательно, по формуле (2) имеем:

Р₁₀₀₀ (11 £ k £ 29)» 0,4788 + 0,4788 = 0,9576.

Пример 3. Телефонная станция обслуживает 400 абонентов. Для каждого абонента вероятность того, что в течение часа он позвонит на станцию равна 0,01. Найдите вероятности следующих событий: а) в течение часа 5 абонентов позвонят на станцию; б) в течение часа не более 4 абонентов позвонят на станцию; в) в течение часа не менее 3 абонентов позвонят на станцию.

Решение. Так как р = 0,01 мало и n = 400 велико, то будем пользоваться приближенной формулой Пуассона при l = 400 × 0,01 = 4.

а) Р₄₀₀ (5)» 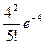» 0,156293; (см. таблицу 4 приложения).

б) Р₄₀₀ (0 £ k £ 4)» 0,018316 + 0,073263 + 0,146525 + 0,195367 + 0,195367 = =0,628838;

в) Р₄₀₀ (3 £ k £ 400) = 1 - Р₄₀₀ (0 £ k £ 4) = 1 – 0,018316 – 0,073263 – 0,146525 = = 0,761896.

Контрольное задание №9

1. Всхожесть семян оценивается вероятностью 0,85. Найдите вероятность того, что из 500 высеянных семян взойдет: а) 425 семян; б) 400 семян; в) 450 семян; г) от 425 до 450 семян.

2. Вероятность того, что покупателю требуется обувь 41-го размера, равна 0,2. Найдите вероятность того, что среди 100 покупателей потребуют обувь 41-го размера: а) 25 человек; б) от 10 до 30 человек; в) не более 30 человек; г) не менее 35 человек.

3. 100 станков работают независимо друг от друга, причем вероятность бесперебойной работы каждого из них в течение смены равна 0,8. Найдите вероятность того, что в течение смены бесперебойно проработают: а) 85 станков; б) от 75 до 85 станков.

4. Вероятность выхода из строя за время t одного конденсатора равна 0,2. Найдите вероятность того, что за время t из 100 независимо работающих конденсаторов выйдут из строя: а) не менее 20 конденсаторов; б) менее 28 конденсаторов; в) от 14 до 26 конденсаторов.

5. Вероятность появления события А в каждом из 1500 независимых испытаний равна р = 0,4. Найдите вероятность того, что число появлений события А заключено между: а) 570 и 630; б) 600 и 660.

6. Вероятность появления события А в каждом из независимых испытаний равна 0,8. Сколько нужно произвести испытаний, чтобы с вероятностью 0,9 можно было ожидать, что событие А появится не менее 75 раз?

7. Вероятность получения положительного результата в каждом из независимых опытов равна 0,9. Сколько нужно произвести опытов, чтобы с вероятностью 0,98 можно было ожидать, что не менее 150 опытов дадут положительный результат?

8. Вероятность производства бракованной детали равна 0,008. Найдите вероятность наиболее вероятного числа бракованных деталей среди наудачу отобранных 100 деталей.

9. Завод отправил на базу 5000 доброкачественных изделий. Вероятность повреждения каждого изделия в пути равна 0,0002. Найдите вероятность того, что среди 5000 изделий в пути будет повреждено: а) ровно 3 изделия; б) ровно одно изделие; в) не более 3 изделий; г) более 3 изделий.

10. Кинотеатр вмещает 730 зрителей. Найдите вероятность того, что: а) 3 зрителя родились в один день (скажем, 1 марта); б) не более 3 зрителей родились в один день.

Дата добавления: 2014-10-22