Формула Бернулли

Тема №8

Опыты a₁, a₂,… называются независимыми, если любая комбинация их исходов является совокупностью независимых событий.

В вероятностной схеме Бернулли рассматривается последовательность n независимых опытов a₁, a₂,…, a_n, в каждом из которых некоторое событие А может наступить с одной и той же вероятностью р = р (А). Условно это событие рассматривается как успех, а его ненаступление (событие ) – как неудача. Вероятность неудачи в каждом опыте равна: q = 1 – p.

Пусть для заданного целого числа k (0 £ k £ n) P_n (k) обозначает вероятность того, что в n опытах успех наступит ровно k раз. Имеет место формула Бернулли:

P_n (k) = 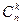p^k q^n-k. (1)

Вероятности P_n (k) (k = 0,1,…, n) называются биномиальными в силу того, что правая часть формулы (1) представляет собой общий член разложения бинома Ньютона:

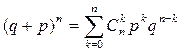. (2)

Так как p+q=1, то из формулы (2) следует, что сумма всех биномиальных вероятностей равна 1:

.

Пример 1. Вероятность попадания в мишень при одном выстреле для данного стрелка равна 0,8 и не зависит от номера выстрела. Требуется найти вероятность того, что при 5 выстрелах произойдет ровно 2 попадания в мишень.

Решение. В этом примере n = 5, р = 0,8 и k = 2; по формуле Бернулли находим: .

Пример 2. 2 равносильных шахматиста играют ряд партий, причем ничьи в счет не идут. Что более вероятно в счете: (1: 1), ил (2: 2), или (3: 3) и т.д.?

Решение. Найдем по формуле Бернулли вероятность того, что в 2n результативных партиях один из шахматистов выиграет n партий, т.е. счет будет n: n. Принимая во внимание, что p = q = , имеем:

.

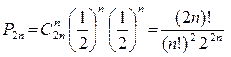Преобразуем полученное выражение с целью найти связь между P_2n(n) и P_2n+2(n+1):

.

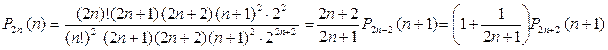Из полученного соотношения

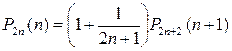(3)

видно, что счет (n: n) более вероятен, чем (n + 1: n + 1). Расчеты по формуле Бернулли показывают, что последовательности событий (1: 1), (2: 2), (3: 3), (4: 4), … соответствует последовательности вероятностей

, , , , …..

То число успехов k₀, которому при заданном n соответствует максимальная биномиальная вероятность P_n(k₀), называется наиболее вероятным числом успехов.

Для нахождения наиболее вероятного числа успехов k₀ по заданным n и р можно воспользоваться неравенствами

np – q £ k₀ £ np + p (4)

или правилом: если число np + p не целое, то k₀ равно целой части этого числа

(k₀ = [np + p]); если же np + p целое, то k₀ имеет два значения 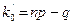и р.

Пример 3. Найдите наиболее вероятное число попаданий в мишень при 5 выстрелах, используя условие примера 1, и соответствующую этому числу вероятность.

Решение. Так как np + p = 5 × 0,8 = 4,8 не целое, то k₀ = [4,8] = 4; вероятность Р₅(4) находим по формуле Бернулли:

.

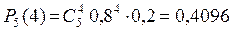Пример 4. Найдите наиболее вероятное число выпаданий герба при 25 бросаниях монеты.

Решение. В этом примере n = 25, p = 0,5. Число np + p = 25 ×0,5+0,5=13 –целое, поэтому 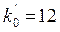и .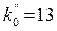

Пусть Р_n (k₁ £ k £ k₂) – вероятность того, что в n опытах схемы Бернулли успех наступит от k₁ до k₂ раз (0 £ k₁ £ k £ n). Тогда имеет место формула

Р_n (k₁ £ k £ k₂) = 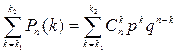; (5)

вероятность Р_n (1 £ k £ n) того, что в n опытах успех наступит хотя бы один раз, равна:

Р_n (1 £ k £ n)= 1 – qⁿ. (6)

Пример 5. Монета брошена 10 раз. Найдите вероятность того, что герб выпадет: а) от 4 до 6 раз; б) хотя бы один раз.

Решение. А) По формуле (5) при n = 10, k₁ = 4, k₂ = 6, p = q = 0,5 получим:

Р₁₀ (4 £ k £ 6) = Р₁₀ (4) + Р₁₀ (5) + Р₁₀ (6) = .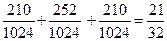

б) По формуле (6) Р₁₀ (1 £ k £ 10) = .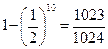

Пример 6. Какое минимальное число опытов достаточно провести, чтобы с вероятностью, не меньшей, чем a (0 < a < 1), можно было бы ожидать наступления успеха хотя бы один раз, если вероятность успеха в одном опыте равна р?

Решение. Потребуем, чтобы вероятность наступления успеха хотя бы один раз в n опытах (см. формулу (6)) была не меньше чем a:

1 – qⁿ ³ a, или 1 – (1 – р)ⁿ ³ a.

Решив полученное равенство относительно n, получаем неравенство

.

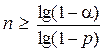Отсюда заключаем, что минимальное число опытов n₀, удовлетворяющее условию примера, равно:

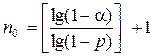. (7)

В частности, если р = 0,02 и a = 0,98, то формула (7) дает n₀ = 80.

Пусть производится n независимых опытов, каждый из которых имеет m (m ³ 2 ) попарно несовместных и единственно возможных исходов А₁, А₂,…, А_m с вероятностями р₁= р(А),…,р_m = (A_m), одинаковыми во всех опытах (имеется в виду, что р₁+р₂+…+ р_m= 1). Для произвольных целых неотрицательных чисел k₁, k₂,…,k_m (k₁+ k₂+…+k_m = n) обозначим через P_n (k₁, k₂,…,k_m) вероятность того, что в n опытах исход А₁ наступит k₁ раз, исход А₂ - k₂ раз и т.д., исход A_m - k_m раз. Тогда справедлива формула

P_n (k₁, k₂,…,k_m) = 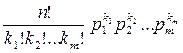, (8)

которая является обобщением формулы Бернулли на случай, когда каждый из независимых опытов a₁, a₂,…, a_n имеет m исходов (m ³ 2 ).

Вероятности P_n (k₁, k₂,…,k_m), соответствующие всевозможным наборам целых неотрицательных чисел k₁, k₂,…,k_m с условием k₁+ k₂+…+k_m = n назовем полиномиальными, ввиду того что выражение, стоящее в правой части формулы (8), представляет собой общий член разложения (р₁+р₂+…+ р_m)ⁿ по полиномиальной формуле.

Вывод формулы (8) аналогичен выводу формулы Бернулли.

Пусть событие В означает: в n независимых опытах событие А_i наступит k₁ раз, событие А₂ - k₂ раз и т.д., событие A_m - k_m раз. Тогда P_n (k₁, k₂,…,k_m) = р(В). Каждый вариант реализации события В можно интерпретировать как строку длины n, составленную из символов А₁, А₂,…, А_m, в которой А_i повторяется k₁ раз, А₂ - k₂ раз и т.д., A_m - k_m раз. Количество N таких строк равно числу размещений состава (k₁, k₂,…,k_m), т.е.

;

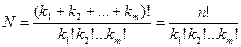вероятность же каждого варианта равна 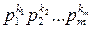. Отсюда по правилу сложения вероятностей имеем (8).

Пример 7. Мишень состоит из 3 попарно непересекающихся зон. При одном выстреле по мишени вероятность попадания в первую зону для данного стрелка равна 0,5. Для второй и третьей зон эта вероятность равна соответственно 0,3 и 0,2. Стрелок произвел 6 выстрелов по мишени. Найдите вероятность того, что при этом окажется 3 попадания в первую зону, 2 попадания во вторую и одно попадание в третью зону.

Решение. В этом примере n = 6, k₁ = 3, k₂ = 2, k₃ = 1, p₁ = 0,5, p₂ = 0,3 и p₃ = 0,2. Подставляя эти данные в формулу (8), получаем искомую вероятность:

Контрольное задание №8

1. Какова вероятность того, что при 8 бросаниях монеты герб выпадет 5 раз?

2. По данным технического контроля 2% изготовленных станков нуждаются в дополнительной регулировке. Найдите вероятность того, что из 6 изготовленных станков 4 нуждаются в дополнительной регулировке.

3. В семье 5 детей. Найдите вероятность того, что среди детей 2 мальчика, если вероятность рождения мальчика принимается 0,5.

4. Найдите наиболее вероятное число выпаданий шестерки при 46 бросаниях игральной кости.

5. Контрольное задание состоит из 10 вопросов, предусматривающих ответы «да» и «нет». Найдите наиболее вероятное число правильных ответов, которые даст учащийся, если он станет выбирать ответ по каждому вопросу наудачу. Найдите вероятность наиболее вероятного числа правильных ответов.

6. Контрольное задание состоит из 10 вопросов, предусматривающих ответы «да» или «нет». Найдите вероятность того, что учащийся, давший 8 правильных ответов, знает 8 вопросов, если известно, что 10% учащихся знают ответы на 6 вопросов, 30% - на 7 вопросов, 30% - на 8 вопросов, а остальные знают ответы не более чем 8 вопросов.

7. Вероятность изготовления стандартной детали 0,95. Сколько деталей должно быть в партии, чтобы наиболее вероятное число нестандартных деталей в ней равнялось 55?

8. Завод изготовляет изделия, каждое из которых с вероятностью 0,01 имеет дефект. Каков должен быть объем случайной выборки с возвращением, чтобы вероятность встретить в ней хотя бы одно дефектное изделие была не меньше 0,95?

9. На автобазе имеется 12 автомашин. Вероятность выхода на линию каждой из них равна 0,8. Найдите вероятность нормальной работы автобазы в ближайший день, если для этого необходимо иметь на линии не меньше 8 автомашин.

10. Вероятность того, что покупателю потребуется обувь 41-го размера, равна 0,2. Найдите вероятность того, что из 5 первых покупателей обувь этого размера понадобится: а) одному; б) по крайней мере одному.

Дата добавления: 2014-10-22