
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение двойного интеграла
|
|
|
|
Механическая и геометрическая трактовки
ТЕМА I. Кратные интегралы
Элементы теории векторных полей
Интегральное исчисление функций нескольких переменных.
Электронный конспект лекций по дисциплине
«Математический анализ»
для студентов II курса
Оглавление
Оглавление. 2
ТЕМА I. Кратные интегралы.. 4
§1. Двойной интеграл: определение, свойства, 4
механическая и геометрическая трактовки. 4
§2. Вычисление двойного интеграла в декартовых и в полярных координатах в двойном интеграле. 10
§3. Тройные интегралы: определение, свойства, механическая трактовка, вычисление в декартовых, в цилиндрических и в сферических координатах 21
§ 4. Приложения двойных и тройных интегралов к задачам геометрии и механики 29
ТЕМА II. Криволинейные и поверхностные интегралы.. 42
§5. Криволинейные интегралы I рода: определение, основные свойства, вычисление, некоторые приложения. 42
§6.Криволинейные интегралы II рода: определение, физическая трактовка, основные свойства, вычисление. 49
§7. Формула Грина. Вычисление площади плоской фигуры с помощью криволинейного интеграла II рода. 58
§ 8. Условия независимости криволинейного интеграла II рода от формы линии интегрирования. 64
§9. Восстановление функции нескольких переменных по ее полному дифференциалу. 72
§10. Поверхностный интеграл I рода: определение, основные свойства, вычисление, некоторые приложения. 77
§11. Поверхностные интегралы II рода: определение, физическая трактовка, основные свойства, вычисление. Формулы Стокса и Остроградского-Гаусса 85
ТЕМА III. Элементы теории векторных полей. 92
§ 12. Определение Векторного поля. Векторные линии. ПОток векторного поля через поверхность: определения, основные свойства, формулы для вычисления 92
§13. Дивергенция и ротор векторного поля: определения, основные свойства, формулы для вычисления. формула остроградского-гаусса в векторной форме 98
§14. Векторный дифференциальный оператор Гамильтона. дифференциальные векторные операции первого и второго порядков. 104
§ 15. Работа и Циркуляция векторного поля: определения, основные свойства циркуляции. 110
§ 16. Потенциальные, соленоидальные и гармонические векторные поля: определения и основные свойства. Нахождение потенциала потенциального векторного поля. 114
Глоссарий. 120
Вопросы для самопроверки. 124
§1. Двойной интеграл: определение, свойства,
Содержание
1.1. Определение двойного интеграла. 5
1.2. Основные свойства двойного интеграла. 6
1.3. Механическая трактовка двойного интеграла. 8
1.4. Геометрическая трактовка двойного интеграла. 8
| Полное определение двойного интеграла | ||||||
2. В каждой части разбиения выберем произвольную точку Pi (xi, yi) и вычислим значение функции f в ней: f ( 3. Составим сумму парных произведений значений функции f (Pi) на площади D Si соответствующих частей разбиения:
эта сумма называется двумерной интегральной суммой функции f(x,y) в области D (двумерной суммой Римана). 4. Вычислим предел интегральной суммы (1) при условии, что ранг разбиения Обозначение и терминология:
D — область интегрирования; f (x,y) — подынтегральная функция; (дифференциал площади плоской области). |
Краткая формулировка определения двойного интеграла (Кратко сформулируйте определение двойного интеграла)
Двойным интегралом от функции f (x,y) по области D называется конечный предел двумерной интегральной суммы, вычисленный при стремлении к нулю ранга разбиения, порождающего эту сумму.
Диаметр плоской фигуры (Что такое диаметр плоской фигуры?)
| Диаметр d плоской геометрической фигуры — это длина наибольшей хорды этой фигуры, то есть наибольшее расстояние между двумя точками этой фигуры. | 
|
Достаточное условие существования двойного интеграла (Сформулируйте достаточное условие существования двойного интеграла)
Если функция z = f(x, y) непрерывна в замкнутой области D, то двойной интеграл от функции f (x, y) по области D существует.
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 963; Нарушение авторских прав?; Мы поможем в написании вашей работы!
 , заданную и непрерывную в замкнутой области D
, заданную и непрерывную в замкнутой области D  XOY.
1. Разобьем область D на n малых элементарных частей произвольным образом. Обозначим через D Si площадь i -ой части, а через di - диаметр i -ой части. Число l = max
XOY.
1. Разобьем область D на n малых элементарных частей произвольным образом. Обозначим через D Si площадь i -ой части, а через di - диаметр i -ой части. Число l = max 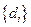 , где i = 1,…, n, назовем рангом разбиения двумерной области D.
, где i = 1,…, n, назовем рангом разбиения двумерной области D.

 ) = f (Pi), i = 1, …, n, (Рис. 1)
) = f (Pi), i = 1, …, n, (Рис. 1)
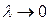 . Если этот предел существует и не зависит от способа разбиения области D на элементарные части и от выбора точек Pi в каждой части, то он называется двойным интегралом от функции f(x,y) по области D.
. Если этот предел существует и не зависит от способа разбиения области D на элементарные части и от выбора точек Pi в каждой части, то он называется двойным интегралом от функции f(x,y) по области D.