Свойства оценок параметров, получаемых МНК

Определение параметров уравнения регрессии α и β проводится по выборке ограниченного характера, поэтому истинные значения параметров получить нельзя. Найденные значения параметров являются статистическими оценками истинных (неизвестных) параметров. Обозначим соответствующие оценки через a и b. Таким образом, оценкой модели 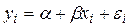является уравнение парной регрессии .

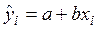В случае, когда условия, высказанные относительно случайной составляющей 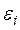выполняются, оценки, полученные методом наименьших квадратов, будут обладать свойствами несмещенности, эффективности и состоятельности.

Оценки параметров являются несмещенными, если математическое ожидание оценки равно истинному значению параметра. Для модели парной регрессии и 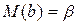. Несмещенность оценок означает, что выборочные оценки параметров концентрируются вокруг истинных неизвестных значений параметров.

Оценки являются эффективными, если они имеют минимальную дисперсию по сравнению с другими несмещенными оценками этого параметра.

Оценки параметров состоятельны, если дисперсия оценки параметра стремится к нулю с возрастанием объема выборки n. Свойство состоятельности означает, что с увеличением объема выборки оценки параметров становятся более надежными в вероятностном смысле, т.е. с увеличением n оценки плотнее концентрируются вокруг истинных неизвестных значений параметров.

Если предположения 2 и 3 относительно случайной составляющей 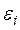не выполняются, то оценки коэффициентов регрессии, найденные по обычному методу наименьших квадратов, будут неэффективными, свойство несмещенности оценок сохраняется.

Дата добавления: 2014-10-22