МНК для модели парной регрессии

Наиболее часто оценку параметров уравнения регрессии осуществляют на основе метода наименьших квадратов (МНК). Согласно МНК для оценки параметров регрессионного уравнения используется следующий критерий:

сумма квадратов отклонений наблюдаемых значений результативного признака от расчетных (теоретических) значений должна быть минимальной:

.

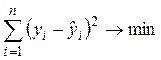Для модели линейной парной регрессии это условие запишется как:

.

Исходными данными для оценки параметров a и b являются наблюдаемые значения зависимой переменной 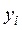и независимых переменных 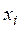. В функции S они представляют собой константы. Переменными в этой функции являются оценки параметров a и b. Необходимым условием существования минимума функции является равенство нулю частных производных по неизвестным параметрам a и b:

, .

Согласно правилам вычисления производных:

,

.

Оптимальные по данному критерию значения оценок в этом случае могут быть найдены решением системы нормальных уравнений, вытекающей из условия равенства нулю частных производных функции S по своим параметрам в точке минимума:

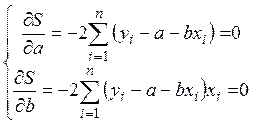или

.

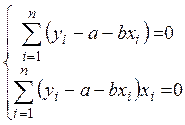Раскрыв скобки, получим стандартную форму нормальных уравнений:

Решая данную систему, найдем искомые оценки параметров уравнения регрессии:

,

.

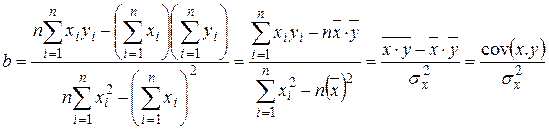Таким образом, МНК дает такие оценки a и b, что найденная прямая проходит через точку с координатами 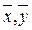. Если начало координат переместить в точку , то система нормальных уравнений упростится и параметр b можно получить следующим образом:

.

Такое решение может существовать только при выполнении условия

, (7.5)

что равносильно отличию от нуля определителя системы нормальных уравнений. Условие (7.5) называется условием идентифицируемости модели наблюдений , и означает, что не все значения совпадают между собой. При нарушении этого условия все точки лежат на одной вертикальной прямой .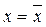

Дата добавления: 2014-10-22