Параметров линейной регрессии

Линейная модель парной регрессии. Оценка значимости

Рассмотрим простейшую линейную модель. Предположим, что имеется выборка n -значений двух переменных: 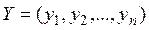- объясняемая переменная и 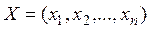- объясняющая переменная. Если между переменными Y и X теоретически существует некоторая линейная зависимость, то ее можно описать в виде уравнения регрессии

. (7.2)

Задача заключается в определении параметров α и β. Уравнение (7.2) будем называть «истинным» уравнением регрессии. В действительности между переменными Y и X наблюдается не столь жесткая линейная связь. Отдельные наблюдения y будут отклоняться от линейной зависимости в силу воздействия различных причин. Обычно зависимая переменная находится под влиянием целого ряда факторов, в том числе и неизвестных исследователю, а также случайных причин (возмущения и помехи). Существенным источником отклонений в ряде случаев являются ошибки измерения. Отклонения от предполагаемой формы связи могут возникнуть и в силу неправильного выбора вида уравнения, описывающего эту зависимость. В дальнейшем будем полагать, что спецификация модели выполнена правильно. Учитывая возможные отклонения, линейное уравнение связи двух переменных (парную регрессию) представим в виде:

, (7.3)

где α - постоянная величина (или свободный член уравнения);

β – коэффициент регрессии, определяющий наклон линии, вдоль которой рассеяны данные наблюдения;

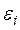- случайная переменная, характеризующая отклонение от теоретически предполагаемой регрессии (случайная составляющая, остаток, возмущение).

Коэффициент регрессии β характеризует изменение переменной 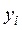при изменении значения 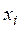на единицу. Если β>0, связь между переменным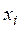и и 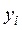прямая, если β <0, то связь обратная.

Случайная составляющая 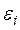отражает тот факт, что изменение 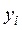будет неточно описываться изменением 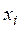, так как присутствуют другие факторы, неучтенные в данной модели.

Таким образом, в уравнении (7.3) значение каждого наблюдения 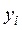представлено как сумма двух частей – систематической 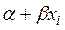и случайной 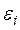. В свою очередь, систематическую часть можно представить в виде уравнения

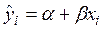, (7.4)

где 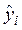характеризует некоторое среднее значение для данного значения x. Соответственно уравнение (7.3) показывает значения с учетом возможных отклонений от средних значений.

Дата добавления: 2014-10-22