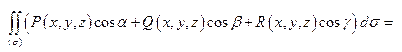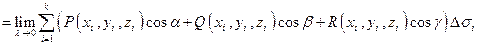КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение и физическая трактовка поверхностного интеграла II рода
|
|
|
|
Некоторые приложения поверхностного интеграла I рода
1. Вычисление площади поверхности (s):
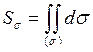
| (3) |
Вычисление площади поверхности
2. Вычисление массы поверхности (s), если известна поверхностная плотность 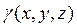 распределения масс:
распределения масс:

| (4) |
Вычисление массы поверхности
Другие механические приложения (вычисление статических моментов, моментов инерции и координат центра масс поверхности) осуществляются аналогично приложениям двойных и тройных интегралов.
Студентам рекомендуется составить формулы этих приложений.
Примеры 2 (приложения поверхностного интеграла I рода)
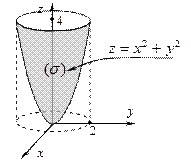
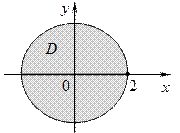
- Найти площадь поверхности части параболоида z = x 2 + y 2 при z £ 4.
Решение
Строим поверхность (s) – указанную часть параболоида и проецируем ее на область 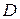 плоскости ХОУ:
плоскости ХОУ:
| 
| 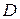 в полярных координатах: в полярных координатах:
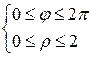
|
Решение
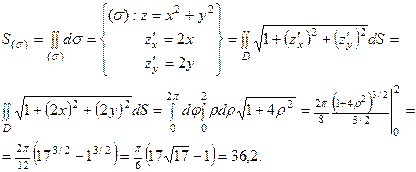
Ответ: 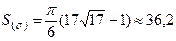 (ед. площади)
(ед. площади)
2. Вычислить массу поверхности куба, на котором 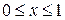 ,
, 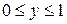 ,
, 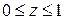 , если поверхностная плотность в точке
, если поверхностная плотность в точке 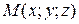 равна
равна 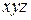 .
.
Решение
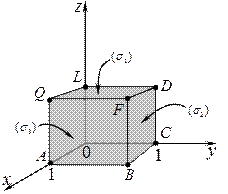
| Масса каждой из трех граней куба, лежащих в координатных плоскостях, равна нулю, так как на каждой из этих граней равна нулю одна из координат  , ,  или или  , поэтому равна нулю плотность распределения массы: , поэтому равна нулю плотность распределения массы:
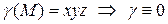 ,
если ,
если 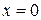 или или 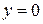 или или 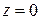 . .
|
Остается вычислить массы трех граней куба, не лежащих в координатных плоскостях:
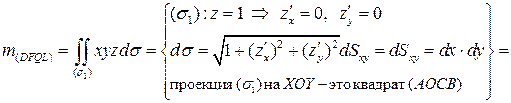
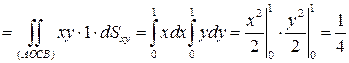 ;
;
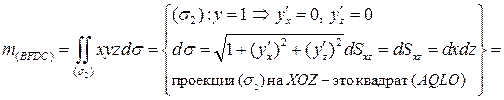
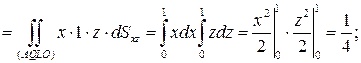

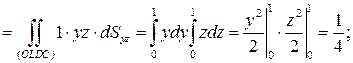
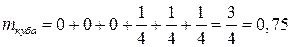 .
.
Ответ: 0,75 (единиц массы).
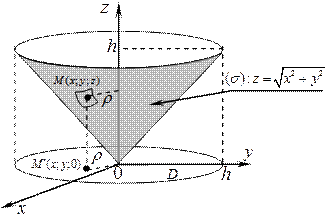
3. Вычислить момент инерции части боковой поверхности конуса 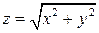 ,
, 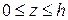 относительно оси OZ, если поверхностная плотность материала
относительно оси OZ, если поверхностная плотность материала 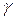 является постоянной.
является постоянной.
Решение
| 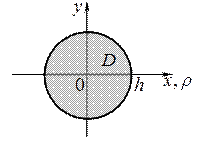
|
Если на боковой поверхности конуса (s) взять бесконечно малый элемент поверхности 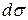 и точку
и точку 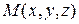 на нем, то его расстояние до оси OZ будет равным
на нем, то его расстояние до оси OZ будет равным 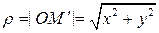 .
.
Тогда момент инерции этого элемента относительно оси OZ будет равен
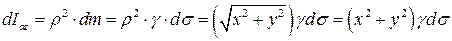 .
.
Момент инерции относительно OZ всей поверхности (s) получится как поверхностный интеграл I рода:
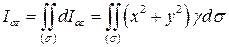 .
.
Вычислим составленный поверхностный интеграл сведением его к двойному интегралу по области 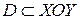 , являющейся проекцией поверхности (s) на координатную плоскость
, являющейся проекцией поверхности (s) на координатную плоскость 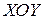 :
:
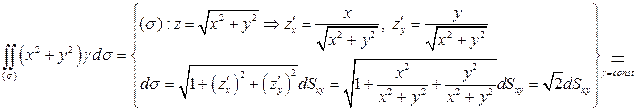

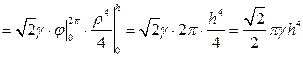 .
.
Ответ: 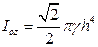 (единиц момента инерции).
(единиц момента инерции).
§11. Поверхностные интегралы II рода: определение, физическая трактовка, основные свойства, вычисление. Формулы Стокса и Остроградского-Гаусса
Содержание
11.1. Определение и физическая трактовка поверхностного интеграла II рода 85
11.2. Основные свойства поверхностного интеграла II рода: 87
11.3. Вычисление поверхностного интеграла II рода. 88
| Определение поверхностного интеграла II рода | ||||
Разбив поверхность (s) на элементарные части с площадями
Каждое из этих парных произведений имеет смысл потока вектора
Вычисляя сумму составленных парных произведений и ее предел при
|
Как и при определении всех предыдущих интегралов, здесь предполагается, что предел существует, является конечным и не зависит ни от способа разбиения поверхности (s) на элементарные части, ни от выбора точки 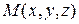 на каждой элементарной части. Кроме этого предполагается, что поверхность (s) является двухсторонней и в каждой ее точке существует вектор нормали
на каждой элементарной части. Кроме этого предполагается, что поверхность (s) является двухсторонней и в каждой ее точке существует вектор нормали 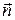 .
.
Определенный равенством (1) интеграл по поверхности (s) можно записать более кратко в векторной форме:
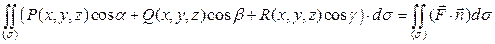
| (1') |
где 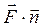 – это скалярное произведение векторов
– это скалярное произведение векторов 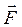 и
и 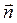 .
.
Очевидно, что при положительных направляющих косинусах будут выполняться равенства:
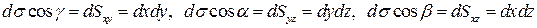
(см. пояснение к формуле (2) предыдущего параграфа).
Поэтому существует еще одна форма записи поверхностного интеграла II рода:
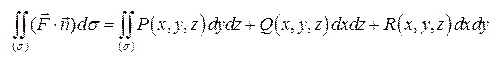
| (2) |
При этом подинтегральное выражение в правой части принято записывать без скобок
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 2676; Нарушение авторских прав?; Мы поможем в написании вашей работы!
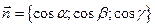 и рассматривается вектор-функция
и рассматривается вектор-функция 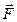 , заданная своими проекциями на оси координат:
, заданная своими проекциями на оси координат: 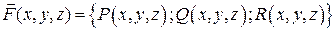 .
.

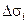 , i = 1,2,..., k и заменив эти части поверхности касательными плоскостями к ним, вычислим следующие парные произведения:
, i = 1,2,..., k и заменив эти части поверхности касательными плоскостями к ним, вычислим следующие парные произведения: .
.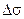 в направлении указанной нормали (Рис. 20).
в направлении указанной нормали (Рис. 20).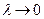 (
(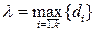 ,
, 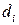 - диаметр i -той части разбиения), получим определение поверхностного интеграла II рода:
- диаметр i -той части разбиения), получим определение поверхностного интеграла II рода: