
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формулировка теоремы о независимости криволинейного интеграла II рода от формы линии интегрирования в трехмерном случае
|
|
|
|
Аналогично доказанной теореме формулируются и доказываются условия независимости криволинейного интеграла II рода от формы линии интегрирования в трёхмерном случае. Приведем здесь только формулировку этих условий.
| Теорема о независимости криволинейного интеграла II рода от формы линии интегрирования (трехмерный случай) |
Для того, чтобы криволинейный интеграл  не зависел от формы линии (АВ), необходимо и достаточно, чтобы выполнялось одно из следующих, эквивалентных между собой, условий:
1.
не зависел от формы линии (АВ), необходимо и достаточно, чтобы выполнялось одно из следующих, эквивалентных между собой, условий:
1.  (1') то есть равен нулю интеграл по любому замкнутому контуру (1') то есть равен нулю интеграл по любому замкнутому контуру 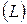 , на котором лежат точки A и B;
2. , на котором лежат точки A и B;
2. 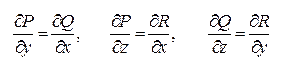 (2') эти три равенства непрерывных частных производных должны выполняться во всех точках некоторой области D, содержащей линию (AB);
3. Существует дифференцируемая функция трех переменных (2') эти три равенства непрерывных частных производных должны выполняться во всех точках некоторой области D, содержащей линию (AB);
3. Существует дифференцируемая функция трех переменных  такая, что подынтегральное выражение является ее полным дифференциалом: такая, что подынтегральное выражение является ее полным дифференциалом:
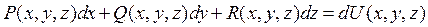 (3') (3')
|
Примеры (вычисление криволинейных интегралов II рода, не зависящих от формы линии интегрирования)
1. Проверить независимость криволинейного интеграла 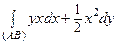
от формы линии (AB) и вычислить его, если A (1;2) и B (3;4).
Решение
Здесь 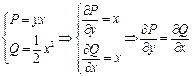 для для   данный криволинейный интеграл не зависит от формы (AB).
данный криволинейный интеграл не зависит от формы (AB).
| 
|
Вычислим его по ломаной (ACB), записав параметрически ее участки (AC) и (CB):


Криволинейный интеграл II рода, не зависящий от формы линии интегрирования, часто записывают так, что указывается только начальная и конечная точки на линии интегрирования.
Ответ: 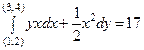 .
.
2. Проверить независимость криволинейного интеграла  от формы линии интегрирования (AB).
от формы линии интегрирования (AB).
Решение
Здесь  ,
,
следовательно, данный криволинейный интеграл зависит от формы линии интегрирования, поэтому для его вычисления нужно дополнительно к имеющемуся условию задачи задавать уравнение линии (AB).
3. Вычислить 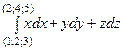
Решение

данный криволинейный интеграл не зависит от формы линии интегрирования.
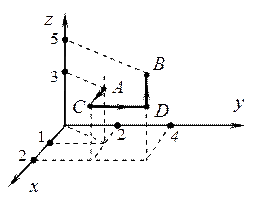
Проще всего такой интеграл вычислять по ломаной линии (ACDB), состоящей из отрезков, параллельных осям координат.

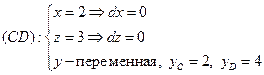

| 
|

Ответ:  .
.
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 734; Нарушение авторских прав?; Мы поможем в написании вашей работы!