Описание решения

Постановка задачи в двумерном случае

Восстановление функции нескольких переменных по ее полному дифференциалу

Содержание

9.1. Постановка задачи в двумерном случае. 72

9.2. Описание решения. 72

Это одно из приложений криволинейного интеграла II рода.

Дано выражение полного дифференциала функции двух переменных:

.

Найти функцию .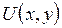

1. Так как не всякое выражение вида 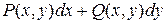является полным дифференциалом некоторой функции U (x, y), то необходимо проверить корректность постановки задачи, то есть проверить необходимое и достаточное условие полного дифференциала, которое для функции 2-х переменных имеет вид 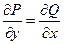. Это условие следует из эквивалентности утверждений (2) и (3) в теореме предыдущего параграфа. Если обозначенное условие выполнено, то задача имеет решение, то есть функцию U (x, y) восстановить можно; если условие не выполнено, то задача не имеет решения, то есть функцию 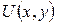восстановить нельзя.

2. Найти функцию 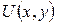по ее полному дифференциалу 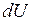можно, например, с помощью криволинейного интеграла II рода, вычислив его от 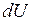по линии, соединяющей фиксированную точку (x ₀, y ₀) и переменную точку (x;y) (Рис. 18):

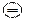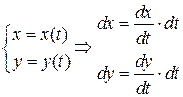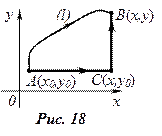
записываем параметрические уравнения любой линии l: и сводим криволинейный интеграл к определённому интегралу

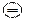
Таким образом получено, что криволинейный интеграл II рода от полного дифференциала dU (x, y) равен разности значений функции U (x, y) в конечной и начальной точках линии интегрирования.

Зная теперь этот результат, нужно подставить вместо dU в криволинейный интеграл выражение 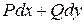и провести вычисление интеграла по ломаной (ACB), учитывая его независимость от формы линии интегрирования:

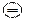
на (AC): 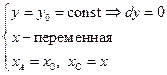на (СВ):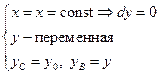

(1)

Таким образом, получена формула, с помощью которой восстанавливается функция 2-х переменных 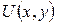по ее полному дифференциалу .

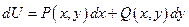3. Восстановить функцию по ее полному дифференциалу можно только с точностью до постоянного слагаемого, так как d (U + const) = dU. Поэтому в результате решения задачи получаем множество функций, отличающихся друг от друга на постоянное слагаемое.

Примеры (восстановление функции двух переменных по ее полному дифференциалу)

1. Найти U (x, y), если dU = (x ² – y ²) dx – 2 xydy.

Решение

Проверяем условие полного дифференциала функции двух переменных:

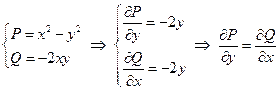— условие полного дифференциала выполнено, значит, функцию U (x, y) восстановить можно.

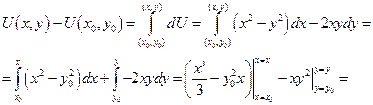
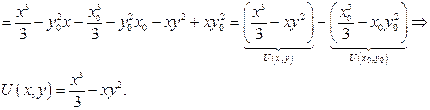
Проверка: 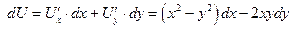– верно.

Ответ: U (x, y) = x ³/3 – xy ² + C.

2. Найти функцию 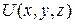, такую что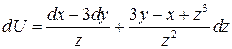

Решение

Проверяем необходимые и достаточные условия полного дифференциала функции трех переменных: 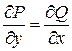, , 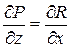, 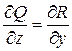если дано выражение .

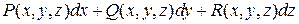В решаемой задаче

, ,

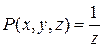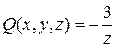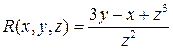
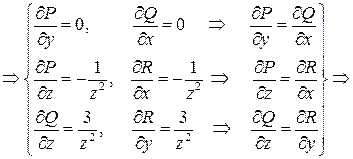
все условия полного дифференциала выполнены, следовательно, функцию 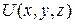восстановить можно (задача поставлена корректно).

Будем восстанавливать функцию 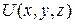с помощью криволинейного интеграла II рода, вычислив его по некоторой линии, соединяющей фиксированную точку 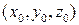и переменную точку 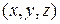, так как

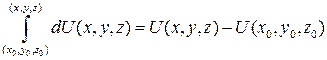
(это равенство выводится так же, как и в двумерном случае).

С другой стороны, криволинейный интеграл II рода от полного дифференциала 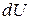не зависит от формы линии интегрирования, поэтому его проще всего считать по ломаной, состоящей из отрезков, параллельных осям координат. При этом в качестве фиксированной точки 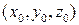можно взять для просто ты взять точку с конкретными числовыми координатами, отслеживая лишь только, чтобы в этой точке и на всей линии интегрирования выполнилось условие существования криволинейного интеграла (то есть чтобы функци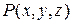и , и 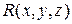были непрерывными). С учетом этого замечания в данной задаче можно взять фиксированной точкой, например, точку М₀. Тогда на каждой из звеньев ломаной будем иметь

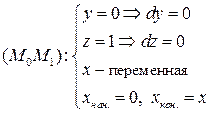на 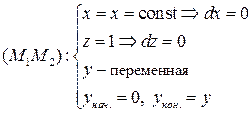, на , на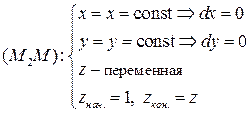

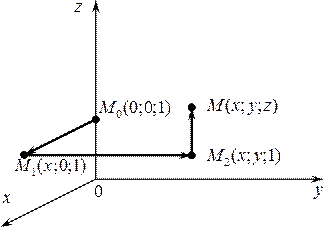
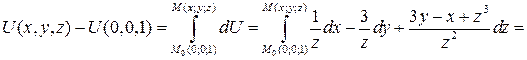
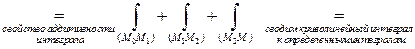
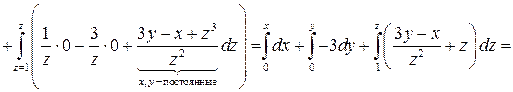
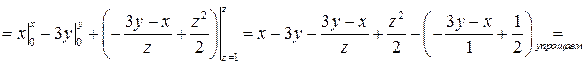
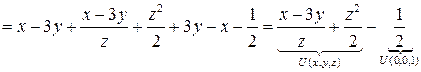
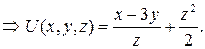
Проверка:

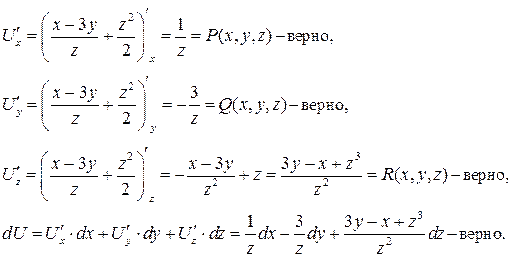
Ответ: 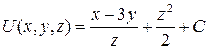, где 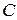- это произвольная постоянная.

§10. Поверхностный интеграл I рода: определение, основные свойства, вычисление, некоторые приложения

Содержание

10.1. Определение и основные свойства поверхностного интеграла I рода. 78

10.2. Вычисление поверхностного интеграла I рода. 79

10.3. Некоторые приложения поверхностного интеграла I рода. 81

Дата добавления: 2014-10-15