Метод последовательных уступок

Понятие о Парето-оптимальном решении.

Между критериями существует область компромисса, содержащая так называемые эффективные или оптимальные по Парето (Парето-оптимальные) решения, для которых невозможно одновременное улучшение всех критериев. Такие решения названы слабо эффективными, а эффективность (или Парето- оптимальность) решения означает, что оно не может быть улучшено по какому-либо критерию f_| без ухудшения ситуации по оставшимся показателям.

Ни один из методов не позволяет выделить единственное оптимальное решение МОЗ (речь, конечно, идет о реализации в общем виде; для конкретного набора весовых коэффициентов получаем единственное частное решение).

Решения, соответствующие различным наборам весовых коэффициентов, являются равноправными элементами множеств Парето-оптимальных и слабо эффективных решений. Однако с практической точки зрения, например, в задачах выбора вариантов в системах автоматизированного проектирования часто требуется выбрать единственное решение (проект). Для этого должна привлекаться некоторая дополнительная информация о предпочтениях лица, принимающего решения. Принцип Парето в этом смысле позволяет лишь сузить класс возможных претендентов на решение и исключить из рассмотрения заведомо неконкурентоспособные варианты. Методы выбора единственного решения многокритериальной задачи существуют и связаны с использованием моделей и процедур, предназначенных для структуризации и количественного описания субъективного мнения лица, принимающего решения, но в данной работе не рассматриваются.

Ниже мы перейдем к подробному рассмотрению перечисленных во традиционных методов многокритериальной оптимизации. Отчасти это объясняется тем, что на многократном применении некоторых из них базируются методы построения Парето-оптимальных и слабо эффективных решений.

Вначале устанавливается предпочтительность всех критериев, при этом на первое место ставится самый важный. При проектировании ГАЛ критериями являются суммарные затраты 3 (минимизируются), производительность ГАЛ Q и гибкость Г (максимизируются). Из этих критериев на первое место можно поставить производительность ГАЛ. Затраты являются скорее ограничением - фирмы (или даже государство) ограничены в своих денежных ресурсах и поэтому могут выделить только 3 < З _mах. Гибкость важна не сама по себе, а постольку, поскольку она может обеспечить надлежащую производительность.

Далее находится оптимальное решение по первому критерию и по нему устанавливается уступка 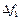. Затем решается задача по второму критерию с дополнительным ограничением, позволяющими первому критерию отклонится от найденного оптимального значения не более чем на уступку 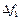. После нахождения оптимального решения по критерию 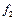по нему назначается уступка 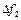и решается задача по третьему критерию с двумя дополнительными ограничениями по первым двум критериям. Аналогично продолжается решение расширенных задач, пока не будет найдено значение наименее важного критерия при уступках по остальным критериям.

Пусть, например, необходимо найти решение задачи по трем критериям: 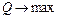, , 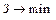, при этом самым важным является критерий Q, на втором месте по важности стоит 3, он более важный, чем Г.

Пусть в результате решения задачи по первому критерию получено, что Q_opt = 155. Допустим, что по этому критерию можно назначить уступку 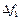= 30. Решим задачу по второму критерию с дополнительным ограничением по первому (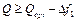= 155-30 = 125). Пусть минимальное значение второго критерия 3_opt = 70, а уступка по нему 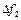=20. Тогда решаем задачу на максимум критерия Г при дополнительных ограничениях по первому и второму критериям. Ограничение по второму критерию: 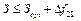=70+20=90.

Если лицо, принимающее решение (ЛПР), устраивают значения всех трех критериев, то задача считается решенной. Если же какие-то значения критериев не устраивают, то изменяются величины уступок и задача решается заново.

Дата добавления: 2014-10-22