Параметрическая оптимизация

Как правило, параметрическая оптимизация относится к оптимизации режимов резания. Параметрическая оптимизация реализует основную цель технологических операций – обработать требуемое количество заготовок по заданным техническим требованием при наименьших затратах труда.

Для оптимизации режимов резания существует 2 подхода: ранняя, статическая оптимизация и динамическая оптимизация.

Статическая оптимизация. В основу берется зависимость «износ – время» (h_з, τ) (рис.1.36), за критерий, как правило, принимается тех­нологический износ, т.е. принцип равного износа, выбирается по качеству обработанной поверхности (шероховатости).

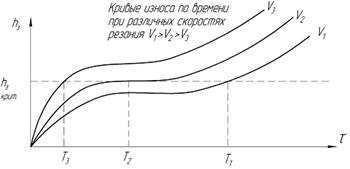
Рисунок 1.36 – Зависимости износа по времени

Кривые «износ – время» получаются экспериментальным путем h_з – τ. Для пар «обрабатываемый материал – инструментальный материал» проводятся опыты по исследованию характера износа инструмента во времени при варьировании скорости резания. Все другие технологические параметры будут постоянными.

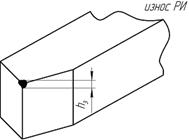
Рисунок 1.37 – Износ режущего инструмента

Технологический критерий износа характеризует требуемое дос­тижимое качество поверхности детали.

В координатах «стойкость – скорость» Т - V (стойкость режущего инструмента до заданного критерия износа) (рис. 1.38) находим величину показателя степени m.

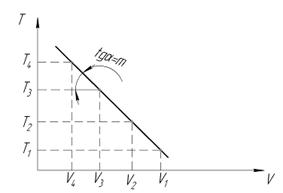
Рисунок 1.38 – Стойкость инструмента до заднего критерия износа

Расчет проводится по обобщенной стойкостной зависимости:

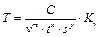, мин

Цель технологической операции – обработать требуемое количе­ство заготовок с заданными техническими требованиями в определенный промежуток времени при наименьших затратах труда.

Применительно к технологической операции затраты на обра­ботку одной заготовки равны:

,

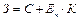где С – себестоимость обработки одной заготовки; 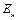– приведенные капитальные вложения в производственные фонды, обусловленные вы­полнением операций; К – нормативный коэффициент эффективности ка­питальных вложений, равен 0,15.

Существует математическое соотношение, связывающее вели­чину приведенных затрат с режимами обработки

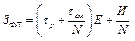, (1.7)

где 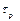– время резания; 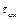– продолжительность простоя станка, связан­ного со сменной режущего инструмента; 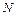– число деталей, обработанных за период стойкости; Е – приведенные затраты на эксплуатацию станка и заработную плату рабочего; И – приведенные затраты, обуслов­ленные эксплуатацией режущего инструмента за период его стойкости, включая затраты на переточку и заработную плату наладчика.

Рассмотрим обработку одинаковых заготовок с постоянными режимами резания. Тогда

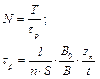, (1.8)

где Т – период стойкости инструмента; 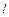– длина обработки; 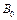– общая ширина обрабатываемой поверхности; В – ширина фрезерования; 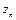– суммарный припуск, снимаемый на данных операциях.

Из выражений (1.7) и (1.8) следует, что приведенные затраты можно найти по предложенной зависимости

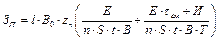. (1.9)

При равномерной обработке значение 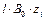в формуле (1.9) может быть опущено как константа.

При однопроходной обработке 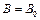, 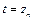и выражение (1.9) упрощается. В то же время период стойкости инструмента надо рассмат­ривать как некоторую функцию режима резания 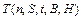, причем Н зависит от условий обработки.

Математически выраженным критерием оптимального режима обработки может служить функция

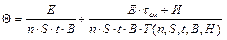. (1.10)

Функцию 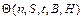называют целевой. Минимум целевой функции (1.10) будет соответствовать минимальным затратам на обра­ботку.

При точении целевую функцию удобнее представить в виде функ­ции аргументов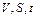

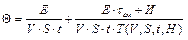. (1.11)

В рассмотренной целевой функции оценку эффективности режимов резания производят по среднему периоду стойкости инструмента.

При обработке с переменными параметрами режима резания (ди­намическая оптимизация) средняя величина затрат, приходящихся на единицу объема удаляемого материала, будет определяться не целевой функцией (1.11), а функционалом

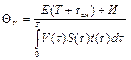, (1.12)

где Т – стойкость режущего инструмента при переменных параметрах процесса обработки.

Понятие функционала относится к вариативному исчислению – это математическая дисциплина, посвященная косвенному поиску экстре­мальных значений. Под функционалом понимается числовая функция, определенная на нескольких классах функций. Примером функционала является интеграл

,

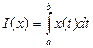где 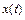– непрерывная функция, определенная на отрезке [a,b].

В основе решения задач оптимальных уравнений лежит матема­тический прием, который носит название “принцип” максимума Понтря­гина, позволяющий найти оптимальное уравнение. Решается при одина­ковых начальных условиях, но при разных уравнениях.

Поскольку связь между величиной износа инструмента и изме­няющимися во времени параметрами режима резания может быть выра­жена только в дифференциальной форме, необходимо внести понятие мгновенной интенсивности износа инструмента

.

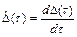При этом величина стойкости Т определяется из соотношения

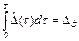(1.13),

где 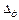– допустимый износ инструмента.

Минимум функционала (1.12) при изменяющихся условиях обработки бут соответствовать некоторому оптимальному значению изменения между интенсивностью удаления припуска и интенсивность расхода ресурса инструмента. Нет четкой взаимосвязи между интенсивностью износа и режимом резания. Рассмотрим это соотношение при стационарных условиях обработки. Интенсивность износа:

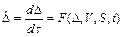. (1.14)

Выясним, можно ли управляя режимом резания эффективно управлять расходом ресурса инструмента. Доя этого необходимо найти такой алгоритм режима резания во времени, который бы обеспечивал минимум приведенных удельных затрат, вычисленных по формуле (1.12). При этом время Т работы инструмента не задано, а определяется граничными условиями: 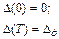(1.15)

Рассматриваемая задача может быть сформулирована следующим образом. Поведение объекта описывается дифференциальным уравнением (1.14). Фазовой координатой является износ 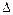, управляемый . Среди всех допустимых решений, переводящих объект из состояния 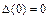в состояние 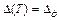, необходимо найти такое, при котором правая часть функционала (1.12) принимает минимальное значение. Для решения используем принцип Понтрягина.

Функционал (1.12) имеет сложный вид, задачу решаем в два этапа. На первом этапе стойкость считается заданной величиной. В этом случае выражение (1.12) достигает минимума при максимуме функционала

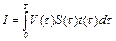. (1.16)

Для зависимостей (1.15) и (1.16) построим функцию Гамильтона-Понтрягина

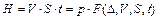, (1.17)

где р – вспомогательная функция времени (присоединительная функция).

Согласно принципу максимума Понтрягина

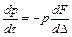. (1.18)

При оптимальном управлении функция Н принимает максимальное значение при соответствующих условиях (каноническое уравнение):

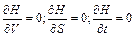. (1.19)

Совместное решение уравнений (1.14), (1.18) и (1.19) при граничных условиях (1.15) дает 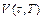, , 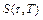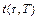. Подставим эти функции в функционал (1.12) после вычисления определенного интеграла в знаменателе получим .

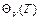На втором этапе находим такое Т, которое соответствует минимуму функции 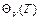и, следовательно, оптимальному управлению. В результате решения находится оптимальная траектория износа режущего инструмента во времени при соответствующих значениях 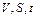, которая будет определять минимальную величину затрат на условную единицу объема удаляемого материала при механической обработке.

Дата добавления: 2014-10-22