Методы оптимизации

В литературе принято различать следующие наиболее распростра­ненные методы оптимизации:

1. Прямая оптимизация является частным случаем оптимизации содним критерием. Она осуществляется при решении простых задач.

Пусть существует некая функция y=f(x), ставим задачу определения минимума данной функции:

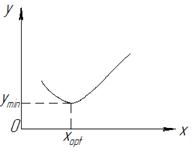
Рисунок 1.28 – Прямая оптимизация

2. Оптимизация с противоположными критериальными зависимостями. Пусть существует две функции вида 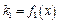и тогда необходимо минимизировать оптимальное решение.

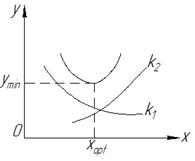
Рисунок 1.29 – Оптимизация с противоположными
критериальными зависимостями

3. Оптимизация с ограниченными критериями. Данный метод основан на методе линейного программирования. Пусть дана некоторая функция (1.1), для которой необходимо найти оптимальное значение.

(1.1)

Для решения задач вводят ограничения на функцию 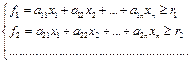(1.2):

(1.2)

Эти ограничения образуют поле ограничений, которое формирует область допустимых значений.

Для практических инженерных целей данную задачу переносят в трехмерное пространство, в этом случае функция имеет следующий вид:

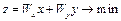(1.3)

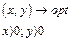(1.4)

Запишем ограничивающие критерии данной функции

(1.5)

Рассмотрим область для решения данной задачи, применим правило эквидистантности, оно имеет следующий вид:

(1.6)

Данное уравнение описывает прямую линию в координатах (х; у). Оптимальное решение находится тогда, когда данная эквидистантная прямая соприкасается с первой точкой области ограничении данной функции (минимум). Последняя точка соприкосновения с областью ограничений соответствует максимуму функции.

4. Оптимизация без экстремума. Рассмотренные первые три случая оптимизации осуществляются с экстремальными критериями. В тоже время существует оптимизация с ограничивающими критериями без условий вы­бора экстремального значения, при этом используются:

· сходящиеся ограничивающие критерии;

· частично расходящиеся ограничивающие критерии.

Рисунок 1.30 – Оптимизация с ограничивающими критериями

Сходящиеся ограничивающие критерии постепенно исключают из возможного множества отдельные его части.

Критерий В более высокого уровня, по сравнению с критерием А, аналогично С по отношению к В.

Пример: А – физическое решение проблемы; В – техническое реше­ние проблемы; С – экономическое решение проблемы.

Рисунок 1.31 – Оптимизация со сходящимися ограничивающими
критериями

При частично расходящихся критериях:

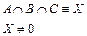
Рисунок 1.32 – Оптимизация с частично расходящимися
критериями

5. Оптимизация с компромиссными критериями. В некоторых случаях для расходящихся критериев можно применить компромиссный критерий. Такой критерий получают путем коррекции основных критериев (рис. 1.32), данный метод имеет квазиоптимальное значение . Оптимума нет. Для решения этой задачи необходимо ввести компромисс между критерием В и С путем их расши­рения, либо изменением координатного положения. Следует добиться условия . В этом случае получим квазиоптимальное решение.

Рисунок 1.33 – Оптимизация с компромиссными критериями

6. Сложная оптимизация (многокритериальная). Оптимизация конструкции, производства, эксплуатации технической системы (изделия) требует использовать комплекса критериев.

На практике мы очень часто имеем дело с однокритериальной оп­тимизацией. Это объясняется значительным влиянием на технические проблемы экономических школ, стараясь свести оценки к денежному из­мерению.

Широкий подход к проблеме технической оптимизации показывает, что чем более удачно выбраны критерии, тем большей оказывается вероятность получения оптимальных технических средств. Критерии ус­танавливают, руководствуясь целесообразностью создания изделия, принципами конструирования, технологическими принципами.

Оптимизируемым объектом может быть не изделие в целом, рас­сматриваемое как техническая система, а лишь та или иная его характе­ристика. Это частичная оптимизация, путь к общей оптимизации.

В то же время существуют подходы к многокритериальной опти­мизации, которые будут рассмотрены ниже в разделе 2.

7. Дивергентно-конвергентная оптимизация. Каждый элемент оптимизации описывается узлом, который представляет собой отдельные стадии создания машины, технологии и т.д. Оптимизационные действия осуществляются на различных стадиях и могут быть расходящимися (ди­вергентными) или сходящимися (конвергентными). Представим в общем виде стадии создания объектов с помощью теории графов.

Рисунок 1.34 – Дивергентно-конвергентная оптимизация

Дивергентные стадии:

1-ая стадия: концептуальное решение проблемы; оптимизация с использованием главного критерия.

2-ая стадия: частные задачи; частичная оптимизация.

3-я стадия: детализация с частичной оптимизацией.

4-ая стадия: предварительная проверка решения задачи.

Подробная теория сетевых графов и примеры решения задач с их использованием рассмотрены во втором разделе.

Дата добавления: 2014-10-22