Критические точки распределения Стьюдента

U

U

T

Z

U

К

Ккр. 0

К

К

0 К_кр.

Рис 8.1. Правосторонняя критическая область.

Критическая Область допустимых

область значений

Рис 8.2. Левосторонняя критическая область.

Критическая Область допустимых Критическая

область значений область

-К_кр. 0 К_кр.

Рис 8.3. Двусторонняя критическая область.

Основной принцип проверки статистических гипотез состоит в следующем:

- если наблюдаемое значение критерия (К_набл.) принадлежит критической области, то нулевая гипотеза Н₀ отклоняется в пользу конкурирующей Н₁;

- если наблюдаемое значение критерия (К_набл.) принадлежит области допустимых значений, то нулевую гипотезу Н₀ нельзя отклонить.

Можно принять решение относительно нулевой гипотезы Н₀ путем сравнения наблюдаемого (К_набл.) и критического значений критерия (К_кр.).

При правосторонней конкурирующей гипотезе:

Если К_набл. £ К_кр., то нулевую гипотезу Н₀ нельзя отклонить;

если К_набл. > К_кр., то нулевая гипотеза Н₀ отклоняется в пользу конкурирующей Н₁.

При левосторонней конкурирующей гипотезе:

Если К_набл. ³ - К_кр., то нулевую гипотезу Н₀ нельзя отклонить;

если К_набл. < - К_кр., то нулевая гипотеза Н₀ отклоняется в пользу конкурирующей Н₁.

При двусторонней конкурирующей гипотезе:

Если - К_кр. £ К_набл. £ К_кр., то нулевую гипотезу Н₀ нельзя отклонить;

если К_набл. > К_кр. или К_набл. < - К_кр., то нулевая гипотеза Н₀ отклоняется в пользу конкурирующей Н₁.

Алгоритм проверки статистических гипотез сводится к следующему:

1. Сформулировать нулевую Н₀ и альтернативную Н₁ гипотезы;

2. Выбрать уровень значимости a;

3. В соответствии с видом выдвигаемой нулевой гипотезы Н₀ выбрать статистический критерий для ее проверки, т.е. - специально подобранную случайную величину К, точное или приближенное распределение которой заранее известно;

4. По таблицам распределения случайной величины К, выбранной в качестве статистического критерия, найти его критическое значение К_кр. (критическую точку или точки);

5. На основании выборочных данных по специальному алгоритму вычислитьнаблюдаемое значение критерия К_набл.;

6. По виду конкурирующей гипотезы Н₁ определить тип критической области;

7. Определить, в какую область (допустимых значений или критическую) попадает наблюдаемое значение критерия К_набл., и в зависимости от этого - принять решение относительно нулевой гипотезы Н₀.

Следует заметить, что даже в том случае, если нулевую гипотезу Н₀ нельзя отклонить, это не означает, что высказанное предположение о генеральной совокупности является единственно подходящим: просто ему не противоречат имеющиеся выборочные данные, однако таким же свойством наряду с высказанной могут обладать и другие гипотезы.

Можно интерпретировать результаты проверки нулевой гипотезы следующим образом:

- если в результате проверки нулевую гипотезу Н₀ нельзя отклонить, то это означает, что имеющиеся выборочные данные не позволяют с достаточной уверенностью отклонить нулевую гипотезу Н₀, вероятность нулевой гипотезы Н₀ больше α, а конкурирующей Н₁ - меньше 1 - α;

- если в результате проверки нулевая гипотеза Н₀ отклоняется в пользу конкурирующей Н₁, то это означает, что имеющиеся выборочные данные не позволяют с достаточной уверенностью принять нулевую гипотезу Н₀, вероятность нулевой гипотезы Н₀ меньше α, а конкурирующей Н₁ - больше 1 - α.

Пример 8.1 В семи случаях из десяти фирма-конкурент компании "А" действовала на рынке так, как будто ей заранее были известны решения, принимаемые фирмой "А". На уровне значимости 0,05 определите, случайно ли это, или в фирме "А" работает осведомитель фирмы-конкурента?

Решение. Для того чтобы ответить на вопрос данной задачи, необходимо проверить статистическую гипотезу о том, совпадает ли данное эмпирическое распределение числа действий фирмы-конкурента с равномерным теоретическим распределением?

Если ходы, предпринимаемые конкурентом, выбираются случайно, т.е. в фирме "А" - нет осведомителя (инсайдера), то число "правильных" и "неправильных" ее действий должно распределиться поровну, т.е. по 5 (10/2). А это и есть отличительная особенность равномерного распределения.

Этот вид статистических гипотез относится к гипотезам о виде закона распределения генеральной совокупности.

Сформулируем нулевую и конкурирующую гипотезы согласно условию задачи.

Н₀: Х~R(a; b) - случайная величина Х подчиняется равномерному распределению с параметрами (a; b) (в контексте задачи - "в фирме "А" - нет осведомителя (инсайдера)"; "распределение числа удачных ходов фирмы-конкурента - случайно").

Н₁: Случайная величина Х не подчиняется равномерному распределению (в контексте задачи - "в фирме "А" - есть осведомитель (инсайдер)"; "распределение числа удачных ходов фирмы-конкурента - не случайно").

В качестве критерия для проверки статистических гипотез о неизвестном законе распределения генеральной совокупности используется случайная величина c². Этот критерий называют критерием Пирсона.

Его наблюдаемое значение () рассчитывается по формуле:

, (8.1)

где m_(эмп.)i - эмпирическая частота i-той группы выборки;

m_(теор.)i - теоретическая частота i-той группы выборки.

Составим таблицу распределения эмпирических и теоретических частот:

m(эмп.)i
m(теор.)i

Найдем наблюдаемое значение :

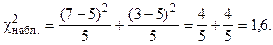
Критическое значение (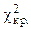) следует определять по таблице распределения c² (см. приложение 4) по уровню значимости a и числу степеней свободы k.

По условию a = 0,05, а число степеней свободы рассчитывается по формуле:

k = n - l -1,

где k - число степеней свободы;

n - число групп выборки;

l - число неизвестных параметров предполагаемой модели, оцениваемых по данным выборки (если все параметры предполагаемого закона известны точно, то l = 0).

По условию задачи число групп выборки (n) равно 2, т.к. могут быть только два варианта действий фирмы-конкурента: "удачные" и "неудачные", а число неизвестных параметров равномерного распределения (l) равно 0.

Отсюда, k = 2 - 0 - 1 = 1.

Найдем 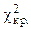по уровню значимости a = 0,05 и числу степеней свободы k=1.

, следовательно, на данном уровне значимости нулевую гипотезу нельзя отклонить, расхождения эмпирических и теоретических частот - незначимые. Данные наблюдений согласуются с гипотезой о равномерном распределении генеральной совокупности.

Это означает, что для утверждения о том, что действия фирмы-конкурента на рынке неслучайны; на уровне значимости a = 0,05 можно утверждать, что в фирме "А" нет платного осведомителя фирмы-конкурента.

Ответ. на уровне значимости a = 0,05 можно утверждать, что в фирме "А" нет платного осведомителя фирмы-конкурента.

Пример 8.2 На уровне значимости a = 0,025 проверить гипотезу о нормальном распределении генеральной совокупности, если известны эмпирические и теоретические частоты:

m(эмп.)i
m(теор.)i

Решение. Сформулируем нулевую и конкурирующую гипотезы согласно условию задачи.

Н₀: Х~N(a; s²) - случайная величина Х подчиняется нормальному закону распределения с параметрами а и s².

Н₁: Случайная величина Х не подчиняется нормальному закону распределения с параметрами а и s².

В качестве критерия для проверки нулевой гипотезы используем критерий Пирсона c².

Найдем наблюдаемое значение ():

Найдем критическое значение критерия (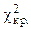) по таблице распределения c² (приложение 4) по уровню значимости a и числу степеней свободы k.

По условию a = 0,025; число степеней свободы найдем по формуле:

k = n - l -1,

где k - число степеней свободы;

n - число групп выборки;

l - число неизвестных параметров предполагаемой модели, оцениваемых по данным выборки.

По условию задачи число групп выборки (n) равно 6, а число неизвестных параметров нормального распределения (l) равно 2.

Отсюда, k = 6 - 2 - 1 = 3.

Найдем 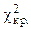по уровню значимости a = 0,025 и числу степеней свободы k=3.

, следовательно, на данном уровне значимости нулевая гипотеза отвергается в пользу конкурирующей, расхождения эмпирических и теоретических частот - значимые. Данные наблюдений не согласуются с гипотезой о нормальном распределении генеральной совокупности.

Ответ. На уровне значимости a = 0,025 данные наблюдений не согласуются с гипотезой о нормальном распределении генеральной совокупности.

Пример 8.3 Техническая норма предусматривает в среднем 40 сек. на выполнение определенной технологической операции на конвейере по производству часов. От работниц, работающих на этой операции, поступили жалобы, что они в действительности затрачивают на эту операцию больше времени. Для проверки данной жалобы произведены хронометрические измерения времени выполнения этой технологической операции у 16 работниц, занятых на этой операции, и получено среднее время выполнения операции = 42 сек. Можно ли по имеющимся хронометрическим данным на уровне значимости a = 0,01 отклонить гипотезу о том, что среднее время выполнения этой операции соответствует норме, если:

а) исправленное выборочное среднее квадратическое отклонение s составило 3,5 сек.;

б) выборочное среднее квадратическое отклонение 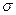составило 3,5 сек.?

Решение. а) Для решения данной задачи необходимо проверить гипотезу о том, что неизвестная генеральная средняя нормальной совокупности точно равна определенному числу, когда дисперсия генеральной совокупности неизвестна ( выборка мала, т.к. n = 16, меньше 30).

Сформулируем нулевую и конкурирующую гипотезы согласно условию задачи.

Н₀: a = а₀ = 40 - неизвестное математическое ожидание а (нормально распределенной генеральной совокупности с неизвестной дисперсией) равно гипотетическому предполагаемому числовому значению а₀ (применительно к условию данной задачи - время выполнения технологической операции соответствует норме).

Н₁: a > 40 - неизвестное математическое ожидание а (нормально распределенной генеральной совокупности с неизвестной дисперсией) больше числовому значению а₀ (применительно к условию данной задачи - время выполнения технологической операции больше установленной нормы).

Так как конкурирующая гипотеза - правосторонняя, то и критическая область - правосторонняя.

В качестве критерия для сравнения неизвестного математического ожидание а (нормально распределенной генеральной совокупности с неизвестной дисперсией) с гипотетическим числовым значением а₀, используется случайная величина t - критерий Стьюдента:

Его наблюдаемое значение (t_набл.) рассчитывается по формуле:

. (8.2)

где - выборочная средняя;

а₀ - числовое значение генеральной средней;

s - исправленное среднее квадратическое отклонение;

n - объем выборки.

Найдем наблюдаемое значение t_набл.:

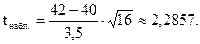
Критическое значение (t_кр.) следует находить по таблице распределения Стьюдента (приложение 5) по уровню значимости a и числу степеней свободы k.

По условию a = 0,01; число степеней свободы найдем по формуле:

k = n - 1,

где k - число степеней свободы;

n - объем выборки.

k = 16 - 1 = 15.

Найдем t_кр. по уровню значимости a = 0,01 (для односторонней критической области) и числу степеней свободы k = 15:

Заметим, что при левосторонней конкурирующей гипотезе Н₁: a < 40 t_кр. следует находить по таблицам распределения Стьюдента (приложение 5) по уровню значимости a (для односторонней критической области) и числу степеней свободы k = n - 1 и присваивать ему "минус";

При двусторонней конкурирующей гипотезе Н₁: a ¹ 40 t_кр. следует находить по таблицам распределения Стьюдента (приложение 5) по уровню значимости a (для двусторонней критической области) и числу степеней свободы k = n - 1).

t_набл. < t_кр, следовательно, на данном уровне значимости нет оснований отклонить нулевую гипотезу.

Ответ. По имеющимся хронометрическим данным на уровне значимости a = 0,01 нельзя отклонить гипотезу о том, что среднее время выполнения этой операции соответствует норме. Следовательно, жалобы работниц - необоснованны.

Область допустимых Критическая

значений область

t

0 t_набл.= 2,29 t_кр.= 2,6

Рис 8.4.

Наблюдаемое значение критерия попадает в область допустимых значений, следовательно, нет оснований отклонить нулевую гипотезу.

б) Для решения данной задачи необходимо проверить гипотезу о том, что неизвестная генеральная средняя нормальной совокупности точно равна определенному числу, когда дисперсия генеральной совокупности неизвестна.

Алгоритм решения задачи будет тот же, что и в первом случае. Однако наблюдаемое значение t_набл. будет рассчитывается по формуле:

. (8.3)

где - выборочная средняя;

а₀ - числовое значение генеральной средней;

- выборочное среднее квадратическое отклонение;

n - объем выборки.

Найдем наблюдаемое значение (t_набл.):

Критическое значение (t_кр.) следует находить по таблице распределения Стьюдента (приложение 5) по уровню значимости a и числу степеней свободы k.

t_набл. < t_кр, следовательно, на данном уровне значимости нет оснований отвергнуть нулевую гипотезу, жалобы работниц - необоснованны.

Ответ. По имеющимся хронометрическим данным на уровне значимости a = 0,01 нельзя отклонить гипотезу о том, что среднее время выполнения этой операции соответствует норме, жалобы работниц - необоснованны.

Пример 8.4 Изменим условие предидущей задачи. Техническая норма предусматривает в среднем 40 сек. на выполнение определенной технологической операции на конвейере по производству часов. От работниц, работающих на этой операции, поступили жалобы, что они в действительности затрачивают на эту операцию больше времени. Для проверки данной жалобы произведены хронометрические измерения времени выполнения этой технологической операции у 36 работниц, занятых на этой операции, и получено среднее время выполнения операции = 42 сек. Можно ли (предполагая время выполнения технологической операции случайной величиной, подчиняющейся нормальному закону) по имеющимся хронометрическим данным на уровне значимости a = 0,01 отклонить гипотезу о том, что среднее время выполнения этой операции соответствует норме, если известно, что среднее квадратическое отклонение генеральной совокупности s составляет 3,5 сек.?

Решение. Для решения данной задачи необходимо проверить гипотезу о том, что неизвестная генеральная средняя нормальной совокупности точно равна числовому значению, когда дисперсия генеральной совокупности известна (большая выборка, т.к. n = 36, больше 30).

Сформулируем нулевую и конкурирующую гипотезы согласно условию задачи.

Н₀: a = а₀ = 40 - неизвестная генеральная средняя нормально распределенной совокупности с известной дисперсией равна числовому значению (применительно к условию данной задачи - время выполнения технологической операции соответствует норме).

Н₁: a > 40 - неизвестная генеральная средняя нормально распределенной совокупности с известной дисперсией больше числового значения (применительно к условию данной задачи - время выполнения технологической операции больше установленной нормы).

Так как конкурирующая гипотеза - правосторонняя, то и критическая область - правосторонняя.

В качестве критерия для сравнения выборочной средней с гипотетической генеральной средней нормальной совокупности, когда дисперсия генеральной совокупности известна, используется случайная величина U:

Его наблюдаемое значение (u_набл.) рассчитывается по формуле:

. (8.4)

где - выборочная средняя;

а₀ - числовое значение генеральной средней;

- выборочное среднее квадратическое отклонение;

n - объем выборки.

Найдем наблюдаемое значение (u_набл.):

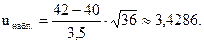
Так как конкурирующая гипотеза - правосторонняя, критическое значение u_кр. следует находить по таблице функции Лапласа (приложение 2) из равенства:

Ф₀(u_кр) = (1 - 2a) / 2.

По условию a = 0,01.

Отсюда:

Ф₀(u_кр) = (1 - 2·0,01) / 2 = 0,49.

По таблице функции Лапласа (приложение 2) найдем при каком u_кр. Ф₀(u_кр) = 0,49.

F₀(2,33) = 0,49.

Следовательно: u_кр. = 2,33.

Заметим, что при левосторонней конкурирующей гипотезе Н₁: a < 40 u_кр. следует находить по таблице функции Лапласа (приложение 2) из равенства Ф₀(u_кр) = (1 - 2a) / 2 и присваивать ему "минус".

При двусторонней конкурирующей гипотезе Н₁: a ¹ 40 u_кр. следует находить по таблице функции Лапласа (приложение 2) из равенства Ф₀(u_кр) = (1 - a) / 2).

u_набл. > u_кр, следовательно, на данном уровне значимости нулевая гипотеза отвергается в пользу конкурирующей. По имеющимся хронометрическим данным с более чем 99%-ной надежностью можно утверждать, что среднее время выполнения этой операции превышает норму. Следовательно, жалобы работниц - обоснованны.

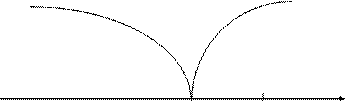
Область допустимых Критическая

значений область

0 u_кр.= 2,33 u_набл.= 3,43

Рис. 8.5.

Наблюдаемое значение критерия попадает в критическую область, следовательно, нулевая гипотеза отвергается в пользу конкурирующей.

Ответ. По имеющимся хронометрическим данным на уровне значимости a = 0,01 можно утверждать, что среднее время выполнения этой операции превышает норму, жалобы работниц - обоснованны.

Пример 8.5 Экономический анализ производительности труда предприятий отрасли позволил выдвинуть гипотезу о наличии двух типов предприятий с различной средней величиной показателя производительности труда. Выборочное обследование 42-х предприятий первой группы дало следующие результаты: средняя производительность труда составила 119 деталей. По данным выборочного обследования 35-и предприятий второй группы средняя производительность труда 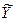составила 107 деталей. Генеральные дисперсии известны: D(X) = 126,91 (дет.²); D(Y) = 136,1 (дет.²). Считая, что выборки извлечены из нормально распределенных генеральных совокупностей Х и Y, на уровне значимости 0,05 проверьте, случайно ли полученное различие средних показателей производительности труда в группах или же имеются два типа предприятий с различной средней величиной производительности труда.

Решение. Для решения данной задачи необходимо сравнить две средние нормально распределенных генеральных совокупностей, генеральные дисперсии которых известны (большие независимые выборки). В данной задаче речь идет о больших выборках, так как n_x = 42 и n_y = 35 больше 30. Выборки - независимые, так как из контекста задачи видно, что они извлечены из непересекающихся генеральных совокупностей.

Сформулируем нулевую и конкурирующую гипотезы согласно условию задачи.

Н₀: 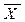= 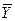- генеральные средние двух нормально распределенных совокупностей с известными дисперсиями равны (применительно к условию данной задачи - предприятия двух групп относятся к одному типу предприятий, - средняя производительность труда в двух группах - одинакова).

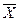Н₁: ¹ 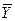- генеральные средние двух нормально распределенных совокупностей с известными дисперсиями не равны (применительно к условию данной задачи - предприятия двух групп относятся к разному типу предприятий, - средняя производительность труда в двух группах - неодинакова).

Выдвигаем двустороннюю конкурирующую гипотезу, так как из условия задачи не следует, что необходимо выяснить больше или меньше производительность труда в одной из групп предприятий по сравнению с другой.

Так как конкурирующая гипотеза - двусторонняя, то и критическая область - двусторонняя.

В качестве критерия для сравнения двух средних генеральных совокупностей, дисперсии которых известны (большие независимые выборки), используется случайная величина Z.

Его наблюдаемое значение (z_набл.) рассчитывается по формуле:

, (8.5)

где - выборочная средняя для X;

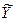- выборочная средняя для Y;

D(X) - генеральная дисперсия для X;

D(Y) - генеральная дисперсия для Y;

n_x - объем выборки для X;

n_y - объем выборки для Y.

Найдем наблюдаемое значение (z_набл.):

Так как конкурирующая гипотеза - двусторонняя, критическое значение (z_кр.) следует находить по таблице функции Лапласа (приложение 2) из равенства:

Ф₀(z_кр) = (1 - a) / 2.

По условию a = 0,05.

Отсюда:

Ф₀(z_кр) = (1 - 0,05) / 2 = 0,475.

По таблице функции Лапласа (приложение 2) найдем при каком z_кр. Ф₀(z_кр) = 0,475.

F₀(1,96) = 0,475.

Учитывая, что конкурирующая гипотеза - двусторонняя, находим две критические точки:

z_{кр.(прав.)} = 1,96; z_{кр.(лев.)} = - 1,96.

Заметим, что при левосторонней конкурирующей гипотезе Н₁: 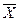<z_кр. следует находить по таблице функции Лапласа (приложение 2) из равенства Ф₀(z_кр) = (1 - 2a) / 2 и присваивать ему "минус".

При правосторонней конкурирующей гипотезе Н₁: >z_кр. следует находить по таблице функции Лапласа (приложение 2) из равенства Ф₀(z_кр) = (1 - 2a) / 2).

z_набл. > z_кр, следовательно, на данном уровне значимости нулевая гипотеза отвергается в пользу конкурирующей. На уровне значимости a = 0,05 можно утверждать, что полученное различие средних показателей производительности труда в группах - неслучайно, имеются два типа предприятий с различной средней величиной производительности труда.

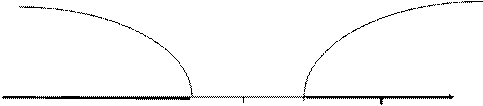Критическая Область допустимых Критическая

область значений область

-z_кр. = -1,96 0 z_кр.= 1,96 z_набл.= 4,565

Рис. 8.6.

Наблюдаемое значение критерия попадает в критическую область, следовательно, нулевая гипотеза отвергается в пользу конкурирующей.

Ответ. На уровне значимости a = 0,05 можно утверждать, что полученное различие средних показателей производительности труда в группах - неслучайно, имеются два типа предприятий с различной средней величиной производительности труда.

Пример 8.6 Предполагается, что применение нового типа резца сократит время обработки некоторой детали. Хронометраж времени обработки 9 деталей, обработанных старым типом резцов, дал следующие результаты: среднее время обработки детали составило 57 мин., исправленная выборочная дисперсия = 186,2 (мин.²). Среднее время обработки 15 деталей, обработанных новым типом резца, 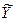по данным хронометражных измерений составило 52 мин., а исправленная выборочная дисперсия = 166,4 (мин.²). На уровне значимости a = 0,01 ответьте на вопрос, позволило ли использование нового типа резцов сократить время обработки детали?

Решение. Для решения данной задачи необходимо сравнить две средние нормально распределенных генеральных совокупностей, генеральные дисперсии которых неизвестны, но предполагаются одинаковыми (малые независимые выборки). В данной задаче речь идет о малых выборках, так как n_x = 9 и n_y = 15 меньше 30. Выборки - независимые, так как из контекста задачи видно, что они извлечены из непересекающихся генеральных совокупностей.

Сформулируем нулевую и конкурирующую гипотезы согласно условию задачи.

Н₀: 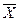= 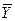- генеральные средние двух нормально распределенных совокупностей с неизвестными дисперсиями (но предполагаемыми одинаковыми) равны (применительно к условию данной задачи - среднее время, затрачиваемое на обработку детали резцами нового и старого типа - одинаково, т.е. использование нового типа резца не позволяет снизить время на обработку детали).

Н₁: 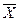> 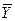- генеральная средняя для Х больше, чем генеральная средняя для Y (применительно к условию данной задачи - среднее время, затрачиваемое на обработку детали резцами старого типа больше, чем - нового, т.е. использование нового типа резца позволяет снизить время на обработку детали).

Так как конкурирующая гипотеза - правосторонняя, то и критическая область - правосторонняя.

Приступать к проверке гипотезы о равенстве генеральных средних двух нормально распределенных совокупностей с неизвестными дисперсиями можно лишь в том случае, если генеральные дисперсии равны. В противном случае, данная задача в теории неразрешима.

Поэтому, прежде чем проверять эту гипотезу, проверим гипотезу о равенстве генеральных дисперсий нормальных совокупностей.

Сформулируем нулевую и конкурирующую гипотезы согласно условию задачи.

Н₀: D(X) = D(Y) - генеральные дисперсии двух нормально распределенных совокупностей равны.

Н₁: D(X) > D(Y) - генеральная дисперсия для X больше генеральной дисперсии для Y. Выдвигаем правостороннюю конкурирующую гипотезу, так как исправленная выборочная дисперсия для Х значительно больше, чем исправленная выборочная дисперсия для Y.

Так как конкурирующая гипотеза - правосторонняя, то и критическая область - правосторонняя.

В качестве критерия для сравнения двух дисперсий нормальных генеральных совокупностей используется случайная величина F - критерий Фишера-Снедекора.

Его наблюдаемое значение (f_набл.) рассчитывается по формуле:

, (8.6)

где 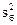- большая (по величине) исправленная выборочная дисперсия;

- меньшая (по величине) исправленная выборочная дисперсия.

Найдем f_набл.:

.

Критическое значение (f_кр.) следует находить по таблице распределения Фишера-Снедекора (приложение 6) по уровню значимости a и числу степеней свободы k₁ и k₂.

По условию a = 0,01; число степеней свободы найдем по формуле:

k₁ = n₁ - 1; k₂ = n₂ - 1,

где k₁ - число степеней свободы большей (по величине) исправленной дисперсии;

k₂ - число степеней свободы меньшей (по величине) исправленной дисперсии;

n₁ - объем выборки большей (по величине) исправленной дисперсии;

n₂ - объем выборки меньшей (по величине) исправленной дисперсии.

Найдем k₁ и k₂:

k₁ = 10 - 1 = 8;

k₂ = 15 - 1 = 14.

Определяем f_кр. по уровню значимости a = 0,01 и числу степеней свободы k₁=9 и k₂=14:

f_набл. < f_кр, следовательно, на данном уровне значимости нет оснований отвергнуть нулевую гипотезу о равенстве генеральных дисперсий нормальных совокупностей.

Следовательно, можно приступить к проверке гипотезы о равенстве генеральных средних двух нормально распределенных совокупностей.

В качестве критерия для проверки этой гипотезы, используется случайная величина t - критерий Стьюдента:

Его наблюдаемое значение (t_набл.) рассчитывается по формуле:

, (8.7)

где - выборочная средняя для X;

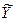- выборочная средняя для Y;

D(X) - генеральная дисперсия для X;

D(Y) - генеральная дисперсия для Y;

n_x - объем выборки для X;

n_y - объем выборки для Y.

Найдем t_набл.:

.

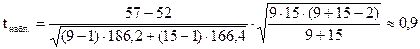Критическое значение (t_кр.) следует находить по таблице распределения Стьюдента (приложение 5) по уровню значимости a и числу степеней свободы k.

По условию a = 0,01; число степеней свободы найдем по формуле:

k = n_x + n_y - 2,

где k - число степеней свободы;

n_x - объем выборки для X;

n_y - объем выборки для Y.

k = 9 + 15 - 2 = 22.

Найдем t_кр. по уровню значимости a = 0,01 (для односторонней критической области) и числу степеней свободы k = 22:

Заметим, что при левосторонней конкурирующей гипотезе 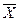<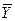t_кр. следует находить по таблицам распределения Стьюдента (приложение 5) по уровню значимости a (для односторонней критической области) и числу степеней свободы k = n_x + n_y - 2 и присваивать ему "минус";

При двусторонней конкурирующей гипотезе 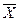¹ 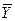t_кр следует находить по таблицам распределения Стьюдента (приложение 5) по уровню значимости a (для двусторонней критической области) и числу степеней свободы k = n_x + n_y - 2).

t_набл. < t_кр, следовательно, на данном уровне значимости нет оснований отвергнуть нулевую гипотезу. По имеющимся хронометрическим данным на уровне значимости a = 0,01 нельзя отклонить гипотезу о том, что генеральные средние равны, т.е. среднее время, затрачиваемое на обработку детали старым и новым типом резцов отличается незначимо, расхождения между средними - случайны, использование нового типа резцов не позволяет снизить время обработки детали.

Область допустимых Критическая

значений область

0 t_набл.= 0,9 t_кр.= 2,51

_{Рис 8.7.}

Наблюдаемое значение критерия попадает в область допустимых значений, следовательно, нулевую гипотезу нельзя отвергнуть.

Ответ. На уровне значимости a = 0,01 нельзя утверждать, что использование нового типа резцов позволило сократить время обработки детали.

Пример 8.7 Партия изделий принимается в том случае, если вероятность того, что изделие окажется соответствующим стандарту, составляет не менее 0,97. Среди случайно отобранных 200 изделий проверяемой партии оказалось 193 соответствующих стандарту. Можно ли на уровне значимости a = 0,02 принять партию?

Решение. Для решения данной задачи необходимо проверить гипотезу о том, что неизвестная генеральная доля точно равна определенному числу.

Сформулируем нулевую и конкурирующую гипотезы согласно условию задачи.

Н₀: р = р₀ = 0,97 - неизвестная генеральная доля р равна р₀ (применительно к условию данной задачи - вероятность того, что деталь из проверяемой партии окажется соответствующей стандарту, равна 0,97; то есть партию изделий можно принять).

Н₁: р < 0,97 - неизвестная вероятность р меньше гипотетической вероятности р₀ (применительно к условию данной задачи - вероятность того, что деталь из проверяемой партии окажется соответствующей стандарту, меньше 0,97; то есть партию изделий нельзя принять).

Так как конкурирующая гипотеза - левосторонняя, то и критическая область - левосторонняя.

В качестве критерия для сравнения наблюдаемой относительной частоты с гипотетической вероятностью появления события используется случайная величина U:

Его наблюдаемое значение (u_набл.) рассчитывается по формуле:

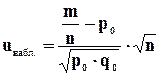, (8.8)

где m / n - относительная частота (частость) появления события;

р₀ - гипотетическая вероятность появления события;

q₀ - гипотетическая вероятность непоявления события;

n - объем выборки.

По условию: m = 193; n = 200; p₀ = 0,97; q₀ = 1 - p₀ = 0,03; a = 0,02.

Найдем наблюдаемое значение (u_набл.):

Так как конкурирующая гипотеза - левосторонняя, то критическое значение (u_кр.) следует находить по таблице функции Лапласа (приложение 2) из равенства:

Ф₀(u_кр) = (1 - 2a) / 2.

По условию a = 0,02.

Отсюда:

Ф₀(u_кр) = (1 - 2 · 0,02) / 2 = 0,48.

По таблице функции Лапласа (приложение 2) найдем при каком u_кр. Ф₀(u_кр) = 0,48.

F₀(2,05) = 0,48.

Учитывая, что конкурирующая гипотеза - левосторонняя, критическому значению необходимо присвоить знак "минус".

Следовательно: u_кр. = - 2,05.

Заметим, что при правосторонней конкурирующей гипотезе Н₁: р > 0,97 u_кр. следует находить по таблице функции Лапласа (приложение 2) из равенства Ф₀(u_кр) = (1 - 2a) / 2.

При двусторонней конкурирующей гипотезе Н₁: p ¹ 0,97 u_кр. следует находить по таблице функции Лапласа (приложение 2) из равенства Ф₀(u_кр) = (1 - a) / 2).

u_набл. > u_кр, следовательно, на данном уровне значимости нет оснований отвергнуть нулевую гипотезу. По имеющимся данным на уровне значимости a = 0,02 нельзя отклонить гипотезу о том, что вероятность того, что изделие окажется соответствующим стандарту, составляет 0,97. Следовательно, партию изделий принять можно.

Критическая Область допустимых

область значений

-u_кр.= - 2,05 u_набл. = - 0,28 0

Рис.8.8.

Наблюдаемое значение критерия попадает в область допустимых значений, следовательно, нет оснований отклонить нулевую гипотезу.

Ответ. На уровне значимости a = 0,02 партию изделий принять можно.

Пример 8.8 Два завода изготавливают однотипные детали. Для оценки их качества извлечены выборки из продукции этих заводов и получены следующие результаты:

	Завод №1	Завод №2
Объем выборки	n1	n2
Число бракованных деталей	m1	m2

На уровне значимости a = 0,025 определите, имеется ли существенное различие в качестве изготавливаемых этими заводами деталей?

Решение. Для решения данной задачи необходимо сравнить две вероятности биномиальных распределений.

Сформулируем нулевую и конкурирующую гипотезы согласно условию задачи.

Н₀: р₁ = р₂ - вероятности появления события в двух генеральных совокупностях, имеющих биномиальное распределение, равны (применительно к условию данной задачи - вероятность того, что деталь изготовленная на первом заводе, окажется бракованной, равна вероятности того, что деталь изготовленная на втором заводе, окажется бракованной).

Н₁: р₁ ¹ р₂ - вероятности появления события в двух генеральных совокупностях, имеющих биномиальное распределение, не равны (применительно к условию данной задачи - вероятность того, что деталь изготовленная на первом заводе, окажется бракованной, не равна вероятности того, что деталь изготовленная на втором заводе, окажется бракованной; заводы изготавливают детали разного качества). Так как по условию задачи не требуется проверить, на каком заводе качество изготавливаемых деталей выше, выдвигаем двустороннюю конкурирующую гипотезу.

Так как конкурирующая гипотеза - двусторонняя, то и критическая область - двусторонняя.

В качестве критерия для сравнения двух вероятностей биномиальных распределений используется случайная величина U:

Его наблюдаемое значение u_набл. рассчитывается по формуле:

, (8.9)

где m₁ / n₁ - относительная частота (частость) появления события в первой выборке;

m₂ / n₂ - относительная частота (частость) появления события во второй выборке;

- средняя частость появления события;

- средняя частость непоявления события;

;

n₁ - объем первой выборки;

n₂ - объем второй выборки.

По условию: m₁ = 20; n₁ = 200; m₂ = 15; n₂ = 300; a = 0,025.

Найдем 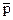- среднюю частость появления события:

.

Найдем 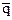- среднюю частость непоявления события:

= 1 - 0,07 = 0,93.

Найдем u_набл.:

Так как конкурирующая гипотеза - двусторонняя, критическое значение (u_кр.) следует находить по таблице функции Лапласа (приложение 2) из равенства:

Ф₀(u_кр) = (1 - a) / 2.

По условию a = 0,025.

Отсюда:

Ф₀(u_кр) = (1 - 0,025) / 2 = 0,4875.

По таблице функции Лапласа (приложение 2) найдем при каком u_кр. Ф₀(u_кр) = 0,4875.

F₀(2,24) = 0,4875.

Учитывая, что конкурирующая гипотеза - двусторонняя, находим две критические точки:

u_{кр.(прав.)} = 2,24; u_{кр.(лев.)} = - 2,24.

Заметим, что при правосторонней конкурирующей гипотезе Н₁: р₁ > р₂ u_кр. следует находить по таблице функции Лапласа (приложение 2) из равенства Ф₀(u_кр) = (1 - 2a) / 2.

При левосторонней конкурирующей гипотезе Н₁: р₁ < р₂ u_кр. следует находить по таблице функции Лапласа (приложение 2) из равенства Ф₀(u_кр) = (1 - 2a) / 2 и присваивать ему знак "минус").

-u_кр. < u_набл. < u_кр, следовательно, на данном уровне значимости нет оснований отвергнуть нулевую гипотезу. По имеющимся данным на уровне значимости a = 0,025 нет оснований отклонить нулевую гипотезу. Следовательно, заводы изготавливают детали одинакового качества.

Критическая Область допустимых Критическая

область значений область

-u_кр. = -2,24 u_набл.= 2,15 u_кр.= 2,24

Рис.8.9.

Наблюдаемое значение критерия попадает в область допустимых значений, следовательно, нет оснований отклонить нулевую гипотезу.

Ответ. Нет оснований отклонить нулевую гипотезу, то есть имеющееся различие в качестве изготавливаемых этими заводами деталей - случайно, незначимо.

Задачи к теме 8

1. Компания, производящая средства для потери веса, утверждает, что прием таблеток в сочетании со специальной диетой позволяет сбросить в среднем в неделю 400 граммов веса. Случайным образом отобраны 25 человек, использующих эту терапию, и обнаружено, что в среднем еженедельная потеря в весе составила 430 граммов со средним квадратическим отклонением - 110 граммов. Проверьте гипотезу о том, что средняя потеря в весе составляет 400 граммов. Уровень значимости a = 0,05.

2. Поступление страховых взносов в 130 филиалов страховых организаций в регионе А составило 260 тыс. у.е., в регионе В на 100 филиалов пришлось 180 тыс. у.е. Дисперсия величины страховых взносов в регионе А равна 65 тыс. у.е., в регионе В – 50 тыс у.е. На уровне значимости a = 0,05 определить существенно ли различается средняя величина поступления страховых взносов в регионах А и В из расчета на 1 филиал.

3. Компания утверждает, что новый вид зубной пасты для детей лучше предохраняет зубы от кариеса, чем зубные пасты, производимые другими фирмами. Для проверки эффекта в случайном порядке была отобрана группа из 400 детей, которые пользовались новым видом зубной пасты. Другая группа из 300 детей, также случайно выбранных, в это же время пользовалась другими видами зубной пасты. После окончания эксперимента было выяснено, что у 30 детей, использующих новую пасту, и 25 детей из контрольной группы появились новые признаки кариеса. Имеются ли у компании достаточные основания для утверждения о том, что новый сорт зубной пасты эффективнее предотвращает кариес, чем другие виды зубной пасты? Принять уровень значимости a = 0,05.

4. Средний размер зарегистрированного капитала кредитных организации на 1.01.2002 г. в Самарской области составил 26 млн.руб. со средним квадратическим отклонением 53 млн.руб., в Ростовской области 46 млн.руб. со средним квадратическим отклонением 61 млн.руб. Число кредитных организаций этих 2-х регионах 23 и 25, соответственно. Существенны ли различия среднего размера уставного капитала кредитных организаций в Самарской и Ростовской областях? Ответ на уровне значимости 0,1.

5. Крупный коммерческий банк заказал маркетинговое исследование по выявлению эффекта «премирования» (калькулятор, набор ручек и др.), как стимула для открытия счета в банке. Для проверки случайным образом было отобрано 200 «премированных» посетителей и 200 «не премированных». В результате выяснилось, что 89% посетителей, которым предлагалась премия и 79% посетителей, которым не предлагалась премия, открыли счет в банке в течение 6 месяцев. Используя эти данные, проверьте гипотезу о том, что доля «премированных» посетителей, открывших счет в банке, статистически существенно отличается от удельного веса «непремированных» посетителей, открывших счет в банке. Принять уровень значимости a = 0,05.

6. Инженер по контролю качества проверяет среднее время горения нового вида электроламп. Для проверки в порядке случайной выборки было отобрано 100 ламп, среднее время горения которых составило 1075 часов. Предположим, что среднее квадратическое отклонение времени горения для генеральной совокупности известно и составляет 100 часов. Используя уровень значимости a = 0,05, проверьте гипотезу о том, что среднее время горения ламп - более 1000 часов.

Предположим, что инженер по контролю качества не имеет информации о генеральной дисперсии и использует выборочное среднее квадратическое отклонение. Изменится ли ответ задачи?

7. Компания, выпускающая в продажу новый сорт растворимого кофе, провела проверку вкусов покупателей по случайной выборке из 400 человек и выяснила, что 220 из них предпочли новый сорт всем остальным. Проверьте на уровне значимости a = 0,01 гипотезу о том, что новый сорт кофе предпочитают 52% потребителей.

8. Страховая компания изучает вероятность дорожных происшествий для подростков, имеющих мотоциклы. За прошедший год проведена случайная выборка 2000 страховых полисов подростков-мотоциклистов и выявлено, что 15 из них попадали в дорожные происшествия и предъявили компании требование о компенсации за ущерб. Может ли аналитик компании отклонить гипотезу, о том, что менее одного процента всех подростков-мотоциклистов, имеющих страховые полисы, попадали в дорожные происшествия в прошлом году? Принять уровень значимости a = 0,05.

9. Новое лекарство, изобретенное для лечения атеросклероза, должно пройти экспериментальную проверку для выяснения возможных побочных эффектов. В ходе эксперимента лекарство принимали 4000 мужчин и 5000 женщин. Результаты выявили, что 60 мужчин и 100 женщин испытывали побочные эффекты при приеме нового медикамента. Можем ли мы на основании эксперимента утверждать, что побочные эффекты нового лекарства у женщин проявляются в большей степени, чем у мужчин? Принять уровень значимости a = 0,05.

10. Руководство фирмы - провайдера полагает, что проведения рекламной акции приведет к увеличению числа новых клиентов. За 30 рабочих дней после проведения рекламной акции число новых клиентов составило 120 чел., тогда как до нее в среднем за день к услугам Internet впервые подключились 10 чел. Считая среднее квадратическое отклонение равным 3, на уровне значимости 0,01 определите принесла ли успех рекламная акция?

11. На начало 2002 г. из 104 филиалов кредитных организаций в Ростовской области 44 были местными и 60 - представляли другие регионы. Существенно ли отличается удельный всех местных филиалов кредитных организаций в Ростовской области от доли местных филиалов в южном федеральном округе, которая на 1.01.2002г. составляла 37,2%? Уровень значимости принять равным 0,05.

12. Компания по производству безалкогольных напитков предполагает выпустить на рынок новую модификацию популярного напитка, в котором сахар заменен сукразитом. Компания хотела бы быть уверенной в том, что не менее 70% её потребителей предпочтут новую модификацию напитка. Новый напиток был предложен на пробу 2000 людей, и 1422 из них сказали, что он вкуснее старого. Может ли компания отклонить предположение о том, что только 70% всех её потребителей предпочтут новую модификацию напитка старой? Принять уровень значимости a = 0,05.

13. Производители нового типа аспирина утверждают, что он снимает головную боль за 30 минут. Случайная выборка 100 человек, страдающих головными болями, показала, что новый тип аспирина снимает головную боль за 28,6 минут при среднем квадратическом отклонении 4,2 минуты. Проверьте на уровне значимости a = 0,05 справедливость утверждения производителей аспирина о том, что это лекарство излечивает головную боль за 30 минут.

14. Производитель утверждает, что система компьютерного контроля готовой продукции исправна. Верно ли это, если допустимый уровень ошибки системы контроля составляет 0,01, а из 10000 проверенных изделий 80 оказались с браком? Ответ дать на уровне значимости 0,01.

15. Выборочная проверка надежности материнских плат 2-х производителей дала следующие результаты: в течения месяца после продажи в 15 из 200 материнских плат производителя А обнаружены дефекты, тогда как среди 400 материнских плат производителя В 8% оказались дефектами. Существенны ли различия в надежности материнских плат производителей А и В? Уровень значимости принять равным 0,01.

16. Годовой оборот 4-х бирж в регионе А составил 120 тыс.у.е.; в регионе В годовой оборот 5-и бирж – 120 тыс. у.е. Исправленное выборочное среднее квадратическое отклонение оборота в регионе А оказалось равным 20 тыс. у.е., в регионе В - 25тыс. у.е. Можно ли на уровне значимости a = 0,05 утверждать, что средний оборот бирж в регионе А больше, чем в регионе В?

17. Компания, занимающаяся консультированием в области инвестиций, заявляет, что среднегодовой процент по акциям определенной отрасли промышленности составляет 11,5%. Инвестор, желая проверить истинность этого утверждения, на основе случайной выборки 50 акций выявил, что среднегодовой процент по ним составил 10,8% с исправленным средним квадратическим отклонением s = 3,4%. На основе имеющейся информации, определите: имеет ли инвестор достаточно оснований, чтобы опровергнуть заявление компании? Принять уровень значимости a = 0,05.

18. Производитель некоторого вида продукции утверждает, что 95% выпускаемой продукции не имеют дефектов. Случайная выборка 100 изделий показала, что только 92 из них свободны от дефектов. Проверьте справедливость утверждения производителя продукции на уровне значимости a = 0,05.

19. Главный бухгалтер большой корпорации провел обследование по данным прошедшего года с целью выяснения доли некорректных счетов. Из 2000 выбранных счетов в 25 оказались некорректные проводки. Для уменьшения доли ошибок он внедрил новую систему. Год спустя он решил проверить, как работает новая система, и выбрал для проверки в порядке случайного отбора 3000 счетов компании. Среди них оказалось 30 некорректных. Можем ли мы утверждать, что новая система позволила уменьшить долю некорректных проводок в счетах? Принять уровень значимости a = 0,05.

20. Владелец фирмы считает, что добиться более высоких финансовых результатов ему помешала неравномерность поставок комплектующих по месяцам года, несмотря на то, что поставщик в полном объеме выполнил свои обязательства за год. Поставщик утверждает, что поставки были не так уж неравномерны. Распределение поставок по месяцам года имеет следующий вид:

Месяцы

Объем поставок, единиц

На уровне значимости a = 0,05 определите кто прав: владелец фирмы или поставщик? Изменится ли ответ на поставленный вопрос, если уровень значимости принять равным 0,01? Объясните результаты.

Л И Т Е Р А Т У Р А

1. Абезгауз Г.Г., Тронь А.П., Коненкин Ю.Н., Коровина И.А. Справочник по вероятностным расчетам. М. 1970.

2. Белинский В.А., Калихман И.А., Майстров Л.Я., Митькин А.М. Высшая математика с основами математической статистики. -М.: Высшая школа, 1965.

3. Вентцель Е.С. Теория вероятностей. - М.: Наука, 1964.

4. Ван-дер-Варден Б.Л. Математическая статистика. М.: Изд-во иностр. лит-ра, 1960.

5. Вайнберг Дж., Шумекер Дж. Статистика. - М.: Статистика, 1979.

6. Вентцель Е.С., Овчаров Л.А. Теория вероятностей (задачи и упражнения). - М.: Наука, 1969.

7. Венецкий И.Г., Кильдишев Г.С. Теория вероятностей и математическая статистика. М., 1975.

8. Венецкий И.Г., Венецкая В.И. Основные математико-статистические понятия и формулы в экономическом анализе. - М.: Статистика, 1974.

9. Гнеденко Б.Г. Курс теории вероятностей. - 6-е изд. - М.: Наука, 1988.

10. Гнеденко Б.В., Хинчин А.Я. Элементарное введение в теорию вероятностей. - М.: Наука, 1970.

11. Гершгорн А.С. Элементы теории вероятностей и математической статистики. Львов, 1961.

12. Гмурман В.Е. Теория вероятностей и математическая статистика. М., 1975.

13. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. - М.: Высшая школа, 1975, 1979, 1997.

14. Гурский Е.И. Теория вероятностей с элементами математической статистики. М.: Высшая школа, 1971.

15. Дружинин Н.К. Математическая статистика в экономике. М., 1971.

16. Емельянов Г.В., Скитович В.П. Задачник по теории вероятностей и математической статистике. - Л.: Изд-во ЛГУ, 1967.

17. Ивашев-Мусатов О.С. Теория вероятностей и математическая статистика. - М.: Наука, 1979.

18. Иванова В.М., Калинина В.Н., Нешумова Л.А., Решетникова И.О. Математическая статистика. - М.: Высшая школа, 1981.

19. Коваленко И.Н., Вилиппова А.А. Теория вероятностей и математическая статистика. - 2-е изд. - М.: Высшая школа, 1982.

20. Карасев А.И., Аксютина З.М., Савельева Т.И. Курс высшей математики для экономических вузов. ч.II. Теория вероятностей и математическая статистика. - М.: Высшая школа, 1982.

21. Колемаев В.А., Староверов О.В., Турундаевский В.Б. Теория вероятностей и математическая статистика. - М.: Высшая школа, 1991.

22. Колемаев В.А., Калинина В.Н. Теория вероятностей и математическая статистика. - М.: ИНФРА-М, 1997.

23. Карасев А.И. Теория вероятностей и математическая статистика. М., 1971.

24. Колде Я.К. Практикум по теории вероятностей и математической статистике. М.: Высшая школа, 1991.

25. Козлова З.А. Методические указания по изучению темы «Закон больших чисел» - Ростов-на-Дону, 1979.

26. Кремер Н.Ш. Теория вероятностей и математическая статистика.-М.: Юнити-Дана,2000

27. Мостллер Ф., Рурке Р., Томас Дж. Вероятность. - М.: Изд-во «Мир», 1969.

28. Маринеску И., Мойнягу Ч., Никулеску Р., Ранку Н., Урсяну В. Основы математической статистики и ее применение. - М.: Статистика, 1970.

29. Павловский З. Введение в математическую статистику. - М.: Статистика, 1967.

30. Румшинский Л.З. Элементы теории вероятностей. М., 1970.

31. Сборник задач по теории вероятностей, математической статистике и теории случайных функций/ под ред. Свешникова А.А.- М.: Наука, 1965.

32. Феллер. В. Введение в теорию вероятностей и ее приложения. - М.: ИЛ, 1952.

33. Чистяков В.П. Курс теории вероятностей.-3-е изд. - М.: Наука, 1987.

34. Четыркин Е.И., Калихман И.Л. Вероятность и статистика. - М.: Финансы и статистика, 1982.

35. Mendenhall W., Wackerly D., Scheaffer R. Mathematical statistics with Applications.- PWS-KENT Publishing Company, USA, 1990.

36. Canavos G. Applied Probability and Statistical Methods. - Little, Brown... Company, USA, 1984.

37. Aczel A. Complete Business Statistics. - 2^nd ed., Richard D. Irwin, INC., 1993.

Приложение 1

Таблица функции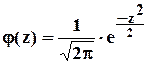

(кривая вероятностей)

x
0,0	0,3989	0,3989	0,3989	0,39

Дата добавления: 2014-10-22