Статистическое оценивание

ВЫБОРОЧНЫЙ МЕТОД И СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ

7.1. Основные понятия и определения выборочного метода

Одно из популярных определений статистики говорит, что это – наука, позволяющая распространять выводы, сделанные на основе изучения части совокупности (случайной выборки), на всю совокупность (генеральную совокупность). В этом определении заключена сущность выборочного метода и его ведущая роль в статистике.

Все единицы совокупности, обладающие интересующими исследователя признаками, составляют генеральную совокупность.

Часть совокупности, случайным образом отобранная из генеральной совокупности – выборочная совокупность – выборка.[2]

Число единиц (элементов) статистической совокупности называется её объёмом. Объем генеральной совокупности обозначается N, а объем выборочной совокупности n. Если объем совокупности велик, то его полагают равным бесконечности.

Случайная выборка из n элементов - это такой отбор, при котором элементы извлекаются по одному из всей генеральной совокупности и каждый из них имеет равный шанс быть отобранным. Требование случайности обеспечивается отбором по таблицам случайных чисел или по жребию. Такая выборка называется собственно-случайной. Одним из примеров использования собственно-случайной выборки является проведение тиражей выигрышей денежно-вещевых лотерей, при которых обеспечивается равная возможность попадания в тираж любого но­мера лотерейного билета.

По способу отбора элементов различают два типа случайных выборок: собственно-случайная повторная выборка (схема возвращенного шара); собст­венно-случайнаябесповторная выборка (схема невозвращенного шара).

Выбор схемы отбора зависит от характера изучаемого объ­екта. Напомним, что при повторном отборе единица наблюдения после извлечения из генеральной совокупности регистрируется и вновь возвращается в генеральную совокупность, откуда опять может быть извлечена случайным образом. При бесповторном отборе отобранный элемент в выборку обратно не возвращается. Необходимо заметить, что независимо от способа организации выборки она должна представлять собой уменьшенную копию генеральной совокупности, то есть быть представительной (репрезентативной).

Пусть из генеральной совокупности извлекается выборка объема n, причем значение признака х₁ наблюдается m₁ раз, х₂ m₂ раз,..., х_k наблюдается m_k раз, 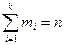- объем выборки.

Мы можем сопоставить каждому значению x_i относительную частоту m_i/n.

Дата добавления: 2014-10-22