Числовые характеристики вариационного ряда

Одной из основных числовых характеристик ряда распределения (вариационного ряда) является средняя арифметическая.

Существует две формулы расчета средней арифметической: простая и взвешенная.

Простую среднюю арифметическую обычно используют, когда данные наблюдения не сведены в вариационный ряд либо все частоты равны единице или одинаковы.

; (6.8)

где x_i - i-е значение признака;

n - объем ряда (число наблюдений; число значений признака).

В том случае, если частоты отличны друг от друга, расчет производится по формуле средней арифметической взвешенной:

; (6.9)

где x_i - i-е значение признака;

m_i - частота i-го значения признака;

k - число значений признака (вариантов).

При расчете средней арифметической в качестве весов могут выступать и частости. Тогда формула расчета средней арифметической взвешенной примет следующий вид:

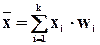(6.10)

где x_i - i-е значение признака;

w_i - частость i-го значения признака;

k - число значений признака (вариантов).

Колеблемость изучаемого признака можно охарактеризовать с помощью различных показателей вариации. К числу основных показателей вариации относятся: дисперсия, среднее квадратическое отклонение, коэффициент вариации.

Дисперсию можно рассчитать по простой и взвешенной формуле.

Простая имеет вид:

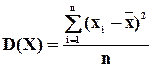. (6.11)

А взвешенная:

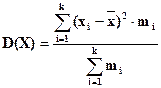. (6.12)

Среднее квадратическое отклонение рассчитывается по формуле:

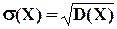(6.13)

Коэффициент вариации рассчитывается по формуле:

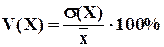. (6.14)

Пример 6.1 При обследовании 50 членов семей рабочих и служащих установлено следующее количество членов семьи: 5; 3; 2; 1; 4; 6; 3; 7; 9; 1; 3; 2; 5; 6; 8; 2; 5; 2; 3; 6; 8; 3; 4; 4; 5; 6; 5; 4; 7; 5; 6; 4; 8; 7; 4; 5; 7; 8; 6; 5; 7; 5; 6; 6; 7; 3; 4; 6; 5; 4.

а) Составьте вариационный ряд распределения частот;

б) Постройте полигон распределения частот, кумуляту;

в) Определите средний размер (среднее число членов) семьи;

г) Охарактеризуйте колеблемость размера семьи с помощью показателей вариации (дисперсии, среднего квадратического отклонения, коэффициента вариации).

Объясните полученные результаты, сделайте выводы.

Решение.а) В данной задаче изучаемый признак является дискретно варьирующим, т.к. размер семей не может отличаться друг от друга менее чем на одного человека. Следовательно, необходимо построить дискретный вариационный ряд.

Чтобы построить вариационный ряд, необходимо подсчитать: сколько раз встречаются те или иные значения признака, и упорядочить их в порядке возрастания или убывания.

Значения изучаемого признака - размер семьи - обозначим x_i, частоты - m_i.

Произведем упомянутые расчеты и запишем полученные результаты в таблице:

xi
mi

б) Дискретный вариационный ряд графически можно представить с помощью полигона распределения частот или частостей.

Построим полигон распределения частот:

Для того чтобы построить кумуляту, необходимо рассчитать накопленные частоты или частости.

Накопленная частота первого варианта х₁ = 1 равна самой частоте этого варианта, т.е. двум: v₁ = 2.

Накопленная частота второго варианта х₂ = 2 равна сумме частот первого и второго вариантов, т.е. v₂ = 2 + 4 = 6.

Далее, аналогично:

v₃ = 12; v₄ = 20; v₅ = 30; v₆ = 39; v₇ = 45; v₇ = 49; v₈ =50.

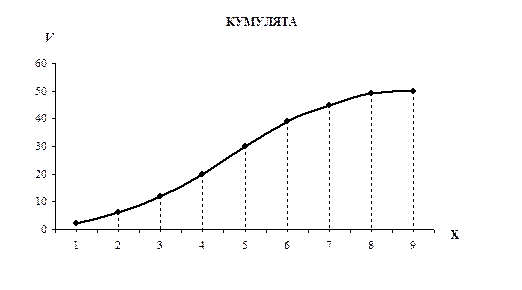Построим кумуляту:

в) Рассчитаем средний размер (среднее число членов) семьи. Так как частоты отличны друг от друга, расчет средней арифметической произведем по формуле (6.9).

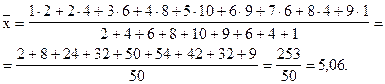
Средний размер семьи - 5,06 человека.

г) Так как частоты - неодинаковы, для расчета дисперсии размера семьи используем формулу (6.12).

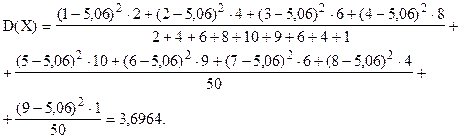
Дисперсия размера семьи - 3,6964 чел².

Найдем среднее квадратическое отклонение размера семьи по формуле (6.13).

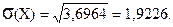
Среднее квадратическое отклонение размера семьи - 1,9226 чел.

Найдем коэффициент вариации размера семьи по формуле (6.14).

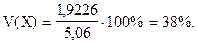
Коэффициент вариации составляет 38%. Так как коэффициент вариации больше 35%, можно сделать вывод о том, что изучаемая совокупность семей является неоднородной, чем и объясняется высокая колеблемость размера семьи в данной совокупности.

Ввиду неоднородности семей, попавших в выборку, использование средней арифметической для характеристики наиболее типичного уровня размера семьи не вполне оправданно - средняя арифметическая нетипична для изучаемой совокупности. В качестве характеристик наиболее типичного уровня размера семьи в данной совокупности лучше использовать моду или медиану.

Пример 6.2 Имеются данные о годовой мощности предприятий цементной промышленности:

Предприятия с годовой мощностью, тыс. тонн	Количество предприятий
до 500
500 – 1000
1000 – 2000
2000 – 3000
свыше 3000

а) Постройте гистограмму, кумуляту;

б) Рассчитайте среднюю мощность предприятий;

в) Найдите дисперсию, среднее квадратическое отклонение, коэффициент вариации.

Объясните полученные результаты, сделать выводы.

Решение.а) Данные о годовой мощности предприятий цементной промышленности представлены в виде интервального вариационного ряда - значения признака заданы в виде интервалов. При этом первый и последний интервалы - открытые: оба интервала не имеют одной из границ. Наконец, данный интервальный вариационный ряд - с неравными интервалами: интервальные разности (разность между верхней и нижней границами интервала) интервалов неодинаковы.

Условно закроем границы открытых интервалов.

Интервальная разность второго интервала равна: 1000 - 500 = 500. Следовательно, нижняя граница первого интервала составит: 500 - 500 = 0.

Интервальная разность предпоследнего интервала равна: 3000 - 2000 = 1000. Следовательно, верхняя граница последнего интервала составит: 3000 + 1000 = 4000.

В результате, получим следующий вариационный ряд:

xi	mi
0 - 500
500 - 1000
1000 - 2000
2000 - 3000
3000 - 4000

Учитывая неодинаковую величину интервалов, для построения гистограммы рассчитаем абсолютные плотности распределения по формуле (6.6).

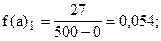
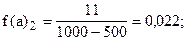
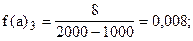
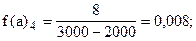
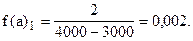
Построим гистограмму:

f(a)			Гистограмма
0,05
0,04
0,03
0,02
0,01
								x

Для того чтобы построить кумуляту, необходимо рассчитать накопленные частоты или частости.

Накопленная частота нижней границы первого варианта х=0 равна нулю. Накопленная частота верхней границы первого интервала равна частоте этого интервала, т.е. 27.

Накопленная частота верхней границы второго интервала равна сумме частот первого и второго интервалов, т.е. 27 + 11 = 38.

Далее, аналогично:

38 + 8 = 46;46 + 8 = 54; 54 + 2 = 56.

Построим кумуляту:

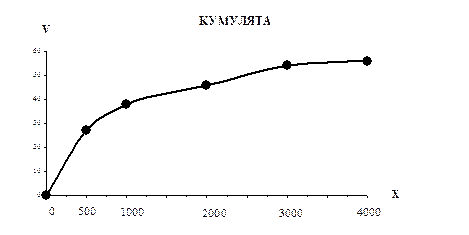б) Рассчитаем среднюю мощность предприятий цементной промышленности.

Так как частоты интервалов - разные, используем для расчета средней арифметической формулу (6.9). При расчете числовых характеристик интервального вариационного ряда в качестве значений признака принимаются середины интервалов.

Рассчитаем середины интервалов:

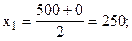
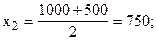
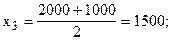
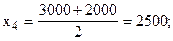
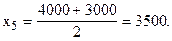
Теперь расчет средней арифметической примет вид:

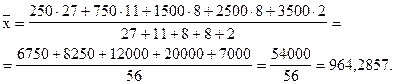
Средняя мощность предприятий цементной промышленности составила 964,2857 тыс. тонн.

Следует отметить, что использование с той или иной целью средней арифметической, рассчитанной по данным интервального ряда с открытыми интервалами, может привести к серьезным ошибкам. Это связано с тем, что открытые интервалы закрываются условно, в действительности значения признака у объектов, попадающих в открытые интервалы, могут выходить далеко за их условные границы.

В связи с этим, для оценки наиболее типичного уровня изучаемого признака по данным интервального ряда с открытыми интервалами лучше использовать моду или медиану.

в) Оценим колеблемость мощности предприятий цементной промышленности.

Так как частоты - неодинаковы, для расчета дисперсии используем формулу (6.12)

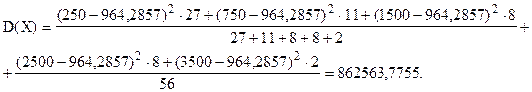
Дисперсия мощности предприятий - 862563,7755 (тыс. тонн)².

Найдем среднее квадратическое отклонение мощности предприятий по формуле (6.13)

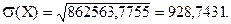
Среднее квадратическое отклонение мощности предприятий - 928,7431 тыс. тонн.

Найдем коэффициент вариации по формуле (6.14)

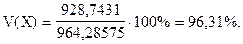
Коэффициент вариации годовой мощности предприятий цементной промышленности составляет 96,31%. Так как коэффициент вариации больше 35%, можно сделать вывод о том, что изучаемая совокупность предприятий является неоднородной, в ее состав вошли и крупные и мелкие предприятия, что и обусловило высокую колеблемость годовой мощности.

Следовательно, использование средней арифметической для характеристики наиболее типичного уровня годовой мощности предприятий цементной промышленности неверно - средняя арифметическая нетипична для изучаемой совокупности. Это еще раз подтверждает необходимость использования моды или медианы для характеристики наиболее типичного уровня годовой мощности данной совокупности предприятий цементной промышленности.

Дата добавления: 2014-10-22