Задачи к теме 5

Учитывая, что вес отобранной туши - нормально распределенная случайная величина, можно быть практически уверенным, что вес случайно отобранной туши не выйдет за пределы от 500 до 1400 кг.

ж) Определим границы, в которых с вероятностью 0,899 будет находиться вес случайно отобранной туши.

Формулу вероятности заданного отклонения нормально распределенной случайной величины Х от своего математического ожидания можно представить следующим образом:

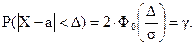
или

где g - вероятность того, что отклонение нормально распределенной случайной величины Х от своего математического ожидания не превысит заданной величины D.

По условию задачи: а = 950; s = 150.

Используя последнюю формулу, получим:

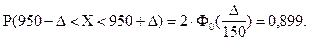
Из соотношения: 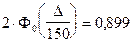, найдем D.

,

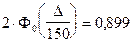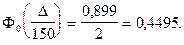
По таблице функции Лапласа (Приложение 2) найдем, при каком z =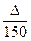

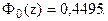
z = 1,64, т.е.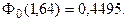

Отсюда: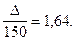

D= 1,64 × 150 = 246.

С вероятностью 0,899 можно ожидать, что отклонение веса случайно отобранной туши от своего математического ожидания не превысит 246 кг.

Найдем границы интересующего нас интервала:

а - D < Х < a + D,

950 - 246 < X < 950 + 246,

704 < X < 1196.

С вероятностью 0,899 можно ожидать, что вес случайно отобранной туши будет находиться в пределах от 704 до 1196 кг.

Ответ:а) 0,02275; б) 0,25143; в) 0,83144; г) 0,2586; д) 0,7414;

е) (500; 1400); ж) 246; (704; 1196).

Пример 5.2. Изменим условие предыдущей задачи.

На рынок поступила крупная партия говядины. Предполагается, что вес туш – случайная величина,

подчиняющаяся нормальному закону распределения с неизвестным математическим ожиданием и средним квадратическим отклонением s =150 кг. Известно, что 37,07% туш имеют вес более 1000 кг. Определите ожидаемый вес случайно отобранной туши.

Решение. По условию задачи: s = 150; a = 1000; b = +¥; P(X > 1000) = 0,3707.

Ожидаемый вес случайно отобранной туши - это среднеожидаемый вес, математическое ожидание, т.е. а =?

Используем формулу (5.10) расчета вероятности попадания в заданный интервал нормально распределенной случайной величины Х:

;

;

;

.

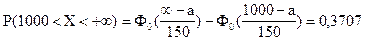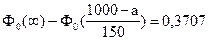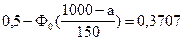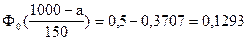По таблице функции Лапласа (Приложение 2) найдем, при каком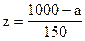

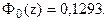
z = 0,33, т.е.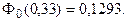

Отсюда: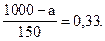

1000 - а = 0,33 × 150 = 50.

а = 1000 - 50 = 950.

Ответ. Среднеожидаемый вес случайно отобранной туши составляет 950 кг.

Пример 5.3. Вновь изменим условие задачи.

На рынок поступила крупная партия говядины. Предполагается, что вес туш - случайная величина, подчиняющаяся нормальному закону распределения с математическим ожиданием а = 950 кг и неизвестным средним квадратическим отклонением. Известно, что 15,87% туш имеют вес менее 800 кг. Определите среднее квадратическое (стандартное) отклонение веса туш.

Решение. По условию задачи: а = 950; a = -¥ b = 800; P(X < 800) = 0,1587; s =?

Используем формулу (5.10) расчета вероятности попадания в заданный интервал нормально распределенной случайной величины Х:

;

;

;

;

.

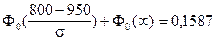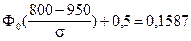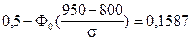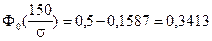По таблице функции Лапласа (Приложение 2) найдем, при каком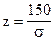

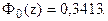
z = 1, т.е.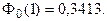

Отсюда: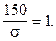

s= 150.

Ответ. Среднее квадратическое отклонение веса туш составляет 150 кг.

Пример 5.4. Еще раз изменим условие задачи.

На рынок поступила крупная партия говядины. Предполагается, что вес туш - случайная величина, подчиняющаяся нормальному закону распределения с неизвестными математическим ожиданием и средним квадратическим отклонением. Известно, что 15,87% туш имеют вес менее 800 кг и 37,07% туш имеют вес более 1000 кг. Определите среднеожидаемый вес и среднее квадратическое (стандартное) отклонение веса туш.

Решение. По условию задачи: a = -¥; b = 800; P(X < 800) = 0,1587;

P(X > 1000) = 0,3707; a =?; s =?

Используем формулу (5.10) расчета вероятности попадания в заданный интервал нормально распределенной случайной величины Х:

;

;

;

;

.

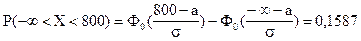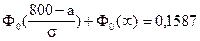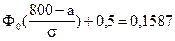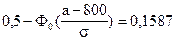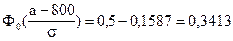По таблице функции Лапласа (Приложение 2) найдем, при каком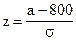

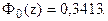
z = 1, т.е.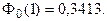

Отсюда: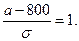

С другой стороны:

;

;

;

.

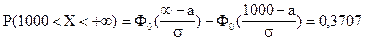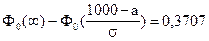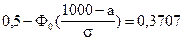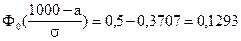По таблице функции Лапласа (Приложение 2) найдем, при каком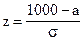

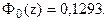
z = 0,33, т.е.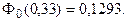

Отсюда: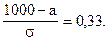

Решим систему линейных уравнений:

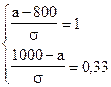
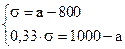
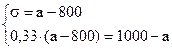
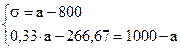
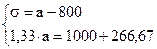
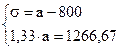
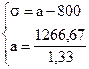
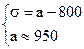
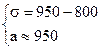
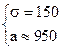
Среднеожидаемый вес случайно отобранной туши составляет 950 кг. Среднее квадратическое отклонение веса туш - 150 кг.

Ответ: а = 950; s = 150.

Пример 5.5. В очередной раз изменим условие задачи.

На рынок поступила крупная партия говядины. Предполагается, что вес туш - случайная величина, подчиняющаяся нормальному закону распределения с математическим ожиданием а = 950 кг и неизвестным средним квадратическим отклонением. Каким должно быть среднее квадратическое (стандартное) отклонение, чтобы с вероятностью 0,81648 можно было утверждать, что абсолютное отклонение веса случайно отобранной туши от математического ожидания не превысит 200 кг?

Решение. По условию задачи: а = 950; D = 200; P(½X - 950½< 200) = 0,81648; s =?

Используем формулу (5.11) расчета вероятности попадания заданного отклонения нормально распределенной случайной величины Х от своего математического ожидания:

Тогда получим:

P(½X - 950½< 200) = 2Ф₀(200 / s) = 0,81648;

2Ф₀(200 / s = 0,81648;

Ф₀(200 / s) = 0,81648 / 2;

Ф₀(200 / s) = 0,40824.

По таблице функции Лапласа (Приложение 2) найдем, при каком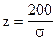

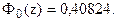
z = 1,33, т.е.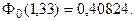

Отсюда: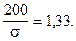

s = 200 / 1,33 = 150.

Ответ. Чтобы с вероятностью 0,81648 можно было утверждать, что абсолютное отклонение веса случайно отобранной туши от математического ожидания не превысит 200 кг, среднее квадратическое отклонение веса туш должно составлять 150 кг.

Пример 5.6 Фирма собирается приобрести партию из 100 000 единиц некоторого товара. Из прошлого опыта известно, что 1% товаров данного типа имеют дефекты. Какова вероятность того, что в данной партии окажется от 950 до 1050 дефектных единиц товара?

Решение. В качестве случайной величины в данной задаче выступает число дефектных единиц товара в общей партии из 100000 единиц. Обозначим ее через X.

Перечислим все возможные значения случайной величины Х: 0, 1, 2,..., 99999, 100000.

Это - дискретная случайная величина, т.к. ее возможные значения отличаются друг от друга не менее чем на 1, и множество ее возможных значений является счетным.

По условию вероятность того, что единица товара окажется дефектной, - постоянна и составляет 0,01 (p = 0,01). Вероятность противоположного события, т.е. того, что единица товара не имеет дефекта - также постоянна и составляет 0,99 (q = 1—p = 1—0,01 = 0,99).

Все 100000 испытаний - независимы, т.е. вероятность того, что каждая единица товара окажется дефектной, не зависит от того, окажется дефектной или нет любая другая единица товара.

Значения случайной величины Х - это, в общем виде, число появлений интересующего нас события в 100000 независимых испытаниях.

Это позволяет сделать вывод о том, что случайная величина Х - число дефектных единиц товара в общей партии из 100000 единиц - подчиняется биномиальному закону распределения вероятностей с параметрами n = 100000 и p = 0,01.

Итак, по условию задачи: n = 100000; p = 0,01; q = 0,99, X = m.

Необходимо найти вероятность того, что число дефектных единиц товара окажется в пределах от m₁ = 950 до m₂ =1050, т.е. - вероятность того, что случайная величина X = m попадет в интервал от 950 до 1050, т.е.:

P(m₁ < m < m₂) =?

Так как мы имеем дело со случайной величиной, подчиняющейся биномиальному распределению, вероятность появления события m раз в n независимых испытаниях необходимо вычислять по формуле Бернулли (4.9).

В данном случае, для определения искомой вероятности нам необходимо с помощью формулы Бернулли найти P_{100000, 950}; P_{100000, 951}; P_{100000, 952};...; P_{100000, 1049}; P_{100000, 1050}, а затем - сложить их, используя теорему сложения вероятностей несовместных событий.

Очевидно, что такой способ определения искомой вероятности связан с громоздкими вычислениями. Так, например:

.

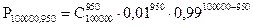Можно значительно облегчить расчеты, если аппроксимировать биномиальное распределение нормальным, т.е. выразить функции биномиального распределения через функции нормального.

Когда n - число испытаний в биномиальном эксперименте - возрастает, дискретное биномиальное распределение стремится к непрерывному нормальному распределению. Это означает, что для больших n мы можем аппроксимировать биномиальные вероятности вероятностями, полученными для нормально распределенной случайной величины, имеющей такое же математическое ожидание и такое же среднее квадратическое отклонение.

Подставим параметры биномиального распределения (5.15) в формулу (5.10) и получим формулу для приближенного расчета вероятности появления события от m₁ и до m₂ раз в n независимых испытаниях P(m₁ < m > m₂):

,

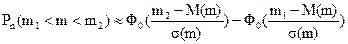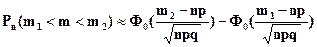, (5.19)

где Ф ₀(z) - функция Лапласа: .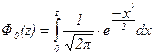

Формулу для приближенного вероятности появления события не менее m₁ и не более m₂ раз в n независимых испытаниях P_n(m₁ < m < m₂) называют интегральной теоремой Лапласа.

Использование локальной и интегральной теорем Лапласа дает приближенные значения искомых вероятностей. Погрешность будет невелика при условии, что

npq > 9.

Для решения данной задачи воспользуемся интегральной теоремой Лапласа:

;

;

;

;

.

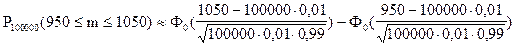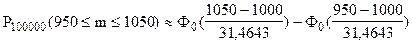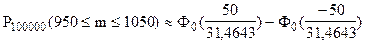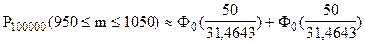По таблице функции Лапласа (Приложение 2) найдем Ф₀(1,59):

Ф₀(1,59) = 0,44408.

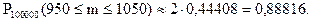
Вероятность того, что в партии из 100000 единиц окажется от 950 до 1050 дефектных единиц товара, составляет 0,88816.

Данную конкретную задачу можно было решить еще более просто.

Математическое ожидание числа дефектных единиц товара равно 1000 единиц:

M(m) = n × p = 100000 × 0,01 = 1000.

Абсолютное отклонение нижней и верхней границ интервала [m₁; m₂] от математического ожидания M(m) = n × p составляет 50 единиц:

½m₁ – n × p½=½950 – 100000 × 0,01½= 50;

½m₂ - n × p½=½1050 – 100000 × 0,01½= 50.

Следовательно, искомую вероятность можно рассматривать как вероятность заданного отклонения частоты от своего математического ожидания:

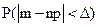
Подставив параметры биномиального распределения в формулу расчета вероятности заданного отклонения нормально распределенной случайной величины от своего математического ожидания, получим формулу для приближенного расчета вероятности заданного отклонения частоты от своего математического ожидания:

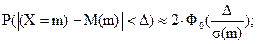
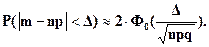(5.20)

При использовании этой формулы для решения задачи сразу получим:

;

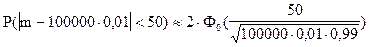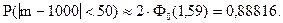
Ответ. Вероятность того, что в партии из 100000 единиц окажется от 950 до 1050 дефектных единиц товара, составляет 0,88816.

Задача 5.7. Подлежат исследованию 400 проб руды. Вероятность промышленного содержания металла в каждой пробе для всех проб одинакова и равна 0,8. Найти вероятность того, что доля проб с промышленным содержанием металла отклонится от вероятности промышленного содержания металла в каждой пробе не более чем на 0,05.

Решение. В отличие от предыдущей задачи, в данном случае речь идет о расчете вероятности заданного отклонения частости (относительной частоты) появления события от вероятности его появления в отдельном независимом испытании, т.е.:

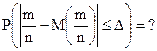
При возрастании числа независимых испытаний распределение частости стремится к нормальному распределению точно так же, как и распределение частоты. Это означает, что при больших n мы можем аппроксимировать распределение частости нормальным распределением случайной величины, имеющей такое же математическое ожидание и такое же среднее квадратическое отклонение.

Подставив параметры распределения частости в формулу расчета вероятности заданного отклонения нормально распределенной случайной величины от своего математического ожидания, получим формулу для приближенного расчета вероятности заданного отклонения частости от своего математического ожидания (вероятности):

Параметры распределения частости:

; ; .

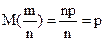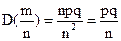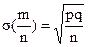Используя эти формулы, получим:

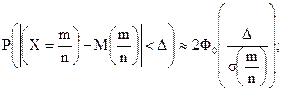
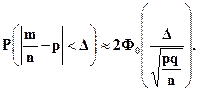(5.21)

Применим данную формулу для решения задачи.

По условию: n = 400; p = 0,8; q = 1- 0,8 = 0,2; D = 0,05.

;

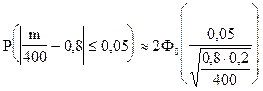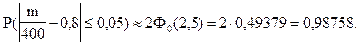
Ответ. Вероятность того, что доля проб с промышленным содержанием металла отклонится от вероятности промышленного содержания металла в каждой пробе не более чем на 0,05, составляет 0,98758.

1. Дневная добыча угля в некоторой шахте распределена по нормальному закону с математическим ожиданием 785 тонн и стандартным отклонением 60 тонн.

а) Найдите вероятность того, что в определенный день будут добыты по крайней мере 800 тонн угля.

б) Определите долю рабочих дней, в которые будет добыто от 750 до 850 тонн угля.

в) Найдите вероятность того, что в данный день добыча угля окажется ниже 665 тонн.

2. Кандидат на выборах считает, что 20% избирателей в определенной области поддерживают его избирательную платформу. Если 64 избирателя случайно отобраны из числа избирателей данной области, найдите вероятность того, что отобранная доля избирателей, поддерживающих кандидата, не будет отличаться по абсолютной величине от истинной доли более, чем на 0,07.

3. Авиакомпании известно, что в среднем 5% людей, делающих предварительный заказ на определенный рейс, не будет его использовать. Если авиакомпания продала 160 билетов на самолет, в котором лишь 155 мест, чему равна вероятность того, что место будет доступно для любого пассажира, имеющего заказ и планирующего улететь?

4. Вес тропического грейпфрута, выращенного в Краснодарском крае, - нормально распределенная случайная величина с неизвестным математическим ожиданием и дисперсией, равной 0,04. Агрономы знают, что 65% фруктов весят меньше, чем 0,5 кг. Найдите ожидаемый вес случайно выбранного грейпфрута.

5. Один из методов, позволяющих добиться успешных экономических прогнозов, состоит в применении согласованных подходов к решению конкретной проблемы. Обычно прогнозом занимается большое число аналитиков. Средний результат таких индивидуальных прогнозов представляет собой общий согласованный прогноз. Пусть этот прогноз относительно величины банковской процентной ставки в текущем году подчиняется нормальному закону со средним значением а = 9% и стандартным отклонением 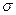= 2,6%. Из группы аналитиков случайным образом отбирается один человек. Найдите вероятность того, что согласно прогнозу этого аналитика уровень процентной ставки:

а) превысит 11%;

б) окажется менее 14%;

в) будет в пределах от 12 до 15%.

6. Предположим, что в течение года цена на акции некоторой компании есть случайная величина, распределенная по нормальному закону с математическим ожиданием, равным 48 условным денежным единицам, и стандартным отклонением, равным 6. Чему равна вероятность того, что в случайно выбранный день обсуждаемого периода цена за акцию была:

а) более 60 условных денежных единиц?

б) ниже 60 за акцию?

в) выше 40 за акцию?

г) между 40 и 50 условных денежных единиц за акцию?

7. Для поступления в некоторый университет необходимо успешно сдать вступительные экзамены. В среднем их успешно сдают лишь 25% абитуриентов. Предположим, что в приемную комиссию поступило 1889 заявлений. Чему равна вероятность того, что хотя бы 500 поступающих сдадут все экзамены (наберут проходной балл)?

8. Средний срок службы коробки передач до капитального ремонта у автомобиля определенной марки составляет 56 месяцев со стандартным отклонением 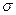= 16 мес. Привлекая покупателей, производитель хочет дать гарантию на этот узел, обещая сделать бесплатно любое число ремонтов коробки передач нового автомобиля в случае ее поломки до определенного срока. Пусть срок службы коробки передач подчиняется нормальному закону. На сколько месяцев в таком случае производитель должен дать гарантию для этой детали, чтобы число бесплатных ремонтов не превышало 2,275% проданных автомобилей?

9. При производстве безалкогольных напитков специальный аппарат разливает определенное число унций (1 унция = 28,3 г) напитка в стандартную ёмкость. Число разлитых унций подчиняется нормальному закону с математическим ожиданием, зависящим от настройки аппарата. Количество унций напитка, разлитых отдельным аппаратом, имеет стандартное отклонение s = 0,4 унции. Пусть ёмкости объёмом в 8 унций наполняются кока-колой. Сколько унций напитка должен в среднем разливать аппарат, чтобы не более 5% ёмкостей оказались переполненными?

10. Фирма, занимающаяся продажей товаров по каталогу, ежемесячно получает по почте заказы. Число этих заказов - есть нормально распределенная случайная величина со средним квадратическим отклонением 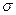= 560 и неизвестным математическим ожиданием. В 90% случаев число ежемесячных заказов превышает 12439. Найдите ожидаемое среднее число заказов, получаемых фирмой за месяц.

11. Еженедельный выпуск продукции на заводе приблизительно распределен по нормальному закону со средним значением, равным 134786 единиц продукции в неделю, и стандартным отклонением - 13000 ед. Найдите вероятность того, что еженедельный выпуск продукции:

а) превысит 150000 единиц;

б) окажется ниже 100000 единиц в данную неделю?

в) Предположим, что возникли трудовые споры, и недельный выпуск продукции стал ниже 80000 ед. Менеджеры обвиняют профсоюз в беспрецедентном падении выпуска продукции, а профсоюз утверждает, что выпуск продукции находится в пределах принятого уровня (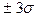). Можно ли доверять профсоюзу?

12. Почтовое отделение быстро оценивает объём переводов в рублях, взвешивая почтовые отправления, полученные в течение каждого текущего рабочего дня. Установлено, что если вес почтовых отправлений составляет N кг, то объём переводов в рублях есть случайная величина, распределенная по нормальному закону со средним значением 160N и стандартным отклонением 20N кг. Найти вероятность того, что в день, когда вес почтовых отправлений составит 150 кг, объём переводов в рублях будет находиться в пределах:

а) от 21000 до 27000 руб.; б) более 28500 руб.; в) менее 22000 руб.

13.Менеджер ресторана по опыту знает, что 70% людей, сделавших заказ на вечер, придут в ресторан поужинать. В один из вечеров менеджер решил принять 20 заказов, хотя в ресторане было лишь 15 свободных столиков. Чему равна вероятность того, что более 15 посетителей придут на заказанные места?

14. Процент протеина в пакете с сухим кормом для собак - нормально распределенная случайная величина с математическим ожиданием 11,2% и стандартным отклонением 0,6%. Производителям корма необходимо, чтобы в 99% продаваемого корма доля протеина составляла не меньше x₁%, но не более x₂%. Найти x₁ и x₂.

15. Вес товаров, помещаемых в контейнер определенного размера, - нормально распределенная случайная величина. Известно, что 65% контейнеров имеют чистый вес больше 4,9 тонн и 25% - имеют вес меньше, чем 4,2 тонны. Найдите ожидаемый средний вес и среднее квадратическое отклонение чистого веса контейнера.

16. Отклонение стрелки компаса из-за влияния магнитного поля в определенной области Заполярья есть случайная величина Х ~N (0; 1²). Чему равна вероятность того, что абсолютная величина отклонения в определенный момент времени будет больше, чем 2,4?

17. Компания А покупает у компании В детали к контрольным приборам. Каждая деталь имеет точно установленное значение размера. Деталь, размер которой отличается от установленного размера более, чем на 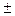0,25 мм, считается дефектной. Компания А требует от компании В, чтобы доля брака не превышала 1% деталей. Если компания В выполняет требование компании А, то каким должно быть допустимое максимальное стандартное отклонение размеров деталей? Учесть, что размер деталей есть случайная величина, распределенная по нормальному закону.

18. Компьютерная система содержит 45 одинаковых микроэлементов. Вероятность того, что любой микроэлемент будет работать в заданное время, равна 0,80. Для выполнения некоторой операции требуется, чтобы, по крайней мере, 30 микроэлементов было в рабочем состоянии. Чему равна вероятность того, что операция будет выполнена успешно?

19. Технический отдел компании, производящей автопокрышки, планирует выпустить несколько экспериментальных партий покрышек и проверить их степень износа на тестирующем оборудовании. С этой целью предполагается увеличивать количество каучука в покрышках каждой последующей партии до тех пор, пока срок службы покрышек окажется приемлемым. Эксперимент показал, что стандартное отклонение срока службы покрышек фактически остается постоянным от партии к партии и составляет 2500 миль (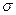= 2500). Если компания хочет, чтобы 80% выпускаемых автопокрышек имели срок службы не менее 25000 миль, то какой наименьший средний срок службы автопокрышек должен быть заложен в расчетах технического отдела? (Считать срок службы автопокрышек нормально распределенным).

20. Менеджер торгово-посреднической фирмы получает жалобы от некоторых клиентов на то, что служащие фирмы затрачивают слишком много времени на выполнение их заказов. Собрав и проанализировав соответствующую информацию. Он выяснил, что среднее время выполнения заказа составляет 6,6 дня, однако для выполнения 20% заказов потребовалось 15 дней и более. Учитывая, что время выполнения заказа есть случайная величина, распределенная по нормальному закону, определить фактическое, стандартное отклонение времени обслуживания клиентов.

Дата добавления: 2014-10-22