График функции распределения

.

.

Рассчитаем значения F(x):

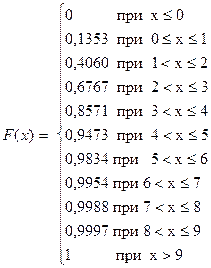
Эти данные можно представить и в виде таблицы:

Таблица 4.6.

X	x £0	0<x£1	1<x£2	2<x£3	3<x£4	4<x£5	5<x£6	6<x£7	7<x£8	8<x£9	x > 9
P(X)		0,1353	0,4060	0,6767	0,8571	0,9473	0,9834	0,9954	0,9988	0,9997

График функции (вероятностная гистограмма)

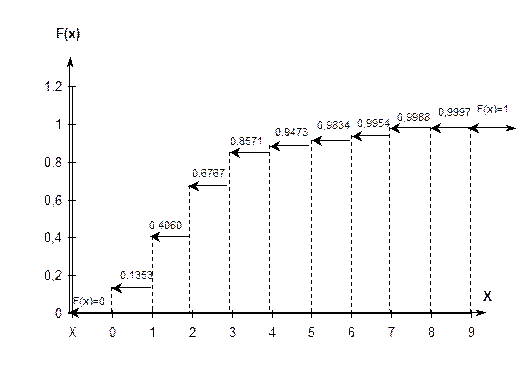
Рис. 4.6.

г) Определим вероятность того, что в течение 15 минут в банк прибудут хотя бы два инкассатора.

“Хотя бы два” - “как минимум два” - “два или больше”. Другими словами, “хотя бы два” - это “или два, или три, или четыре, или...”.

Исходя из этого, для определения вероятности того, что в течение 15 минут в банк прибудут хотя бы два инкассатора, можно использовать теорему сложения вероятностей несовместных событий:

P(X 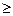2) = P(X = 2) + P(X = 3) + P(X = 4) +... + Р(Х = n).

С другой стороны, все возможные значения случайной величины образуют полную группу событий, а сумма их вероятностей равна 1. По отношению к событию (Х ³ 2) до полной группы событий не хватает события (Х < 2), т. е. (х 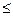1), которое является противоположным событию (Х ³ 2). Поэтому искомую вероятность того, что в течение 15 минут в банк прибудут на автомобиле хотя бы два инкассатора, проще найти следующим образом:

P(X ³ 2) = 1 - P(X £ 1) = 1 - (P(X = 0) + P(X=1)) = 1 - (0,1353 + 0,2707) = 1 - 0,406 =

= 0,594.

Вероятность того, что в течение 15 минут в банк прибудут на автомобиле хотя бы два инкассатора, составляет 0,5904.

д) Определим вероятность того, что в течение 15 минут число прибывших инкассатор окажется меньше трех.

“Меньше трех” - это “или ноль, или один, или два”.

Из теоремы сложения вероятностей несовместных событий следует:

P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2).

P(X < 3) = 0,1353 + 0,2707 + 0,2707 = 0,6767.

Ответ. Вероятность того, что в течение 15 минут в банк прибудет меньше трех инкассаторов, составляет 0,6767.

Пример 4.3. Из 20 лотерейных билетов выигрышными являются 4. Наудачу извлекаются 4 билета.

а) Составьте ряд распределения числа выигрышных билетов среди отобранных;

б) Найдите числовые характеристики этого распределения;

в) Напишите функцию распределения числа выигрышных билетов среди отобранных и постройте ее график;

г) Определите вероятность того, что среди отобранных 4 билетов окажется не меньше трех выигрышных билетов;

д) Определите вероятность того, что среди отобранных 4 билетов окажется не больше одного выигрышного билета.

Решение. В качестве случайной величины в данной задаче выступает число выигрышных билетов среди отобранных. Обозначим ее через X.

Перечислим все возможные значения случайной величины Х: 0, 1, 2, 3, 4.

Это - дискретная случайная величина, т.к. ее возможные значения отличаются друг от друга не менее чем на 1, и множество ее возможных значений является счетным.

Очевидно, что отбор лотерейных билетов - бесповторный. Следовательно, испытания - зависимые.

Вышеперечисленные признаки указывают на то, что рассматриваемая случайная величина - число выигрышных билетов среди отобранных - подчиняется гипергеометрическому закону распределения.

Изобразим ситуацию на схеме:

N

M N-M

n

m n-m

Рис. 4.7.

Случайная величина, интересующая нас, Х = m - число выигрышных билетов в выборке объемом в n билетов. Число всех возможных случаев отбора n билетов из общего числа N билетов равно числу сочетаний из N по n (С), а число случаев отбора m выигрышных билетов из общего числа M выигрышных билетов (и значит, (n-m) проигрышных из общего числа (N - M) проигрышных) равно произведению

С × С(отбор каждого из m выигрышных билетов может сочетаться с отбором любого из (n-m) проигрышных). Событие, вероятность которого мы хотим определить, состоит в том, что в выборке из n лотерейных билетов окажется ровно m выигрышных. По формуле для расчета вероятности события в классической модели вероятность получения в выборке m выигрышных билетов (то есть вероятность того, что случайная величина Х примет значение m) равна:

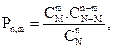
где С- общее число всех единственно возможных, равновозможных и несовместных исходов,

С × С- число исходов, благоприятствующих наступлению интересующего нас события;

m £ n, если n £ M и m £ M, если M < n.

Если по этой формуле вычислить вероятности для всех возможных значений m и поместить их в таблицу, то получим ряд распределения.

а) Составим ряд распределения.

Вычислим вероятности того, что случайная величина примет каждое из своих возможных значений и запишем полученные результаты в таблицу.

По условию задачи N =20; M = 4; n = 4; m = 0, 1, 2, 3, 4.

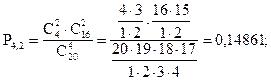
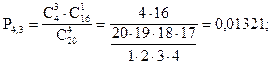
Занесем полученные результаты в таблицу:

Таблица 4.7.

X
P(X)	0,37564	0,46233	0,14861	0,01321	0,00021

Произведем проверку. Так как все возможные значения случайной величины образуют полную группу событий, сумма их вероятностей должна быть равна 1.

Проверка: 0,37564 + 0,46233 + 0,14861 + 0,01321 + 0,00021 = 1.

График полученного распределения вероятностей дискретной случайной величины - полигон распределения вероятностей; изображенный на рис 4.8

Рис. 4.8.

б) Найдем основные числовые характеристики распределения данной случайной величины.

Можно рассчитать математическое ожидание, дисперсию и среднее квадратическое отклонение по общим для любой дискретной случайной величины формулам.

Но математическое ожидание случайной величины, подчиняющейся гипергеометрическому распределению, может быть рассчитано по более простой формуле:

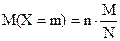
Рассчитаем математическое ожидание числа выигрышных билетов среди отобранных:

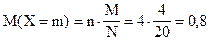(билета).

Дисперсию случайной величины, подчиняющейся распределению, также может быть рассчитано по более простой формуле:

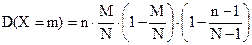
Вычислим дисперсию числа выигрышных билетов среди отобранных:

D(X = m) = 0,53895 (кв.ед.).

Рассчитаем среднее квадратическое отклонение числа выигрышных билетов среди отобранных:

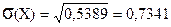3 (билета).

в) Зададим дискретную случайную величину в виде функции распределения:

Рассчитаем значения F(х):

Эти данные можно представить и в виде таблицы:

Таблица 4.8.

X	x £ 0	0 < x £1	1 < x £ 2	2 < x £3	3 < x £ 4	x > 4
F(x)		0,37564	0,83797	0,98658	0,99979

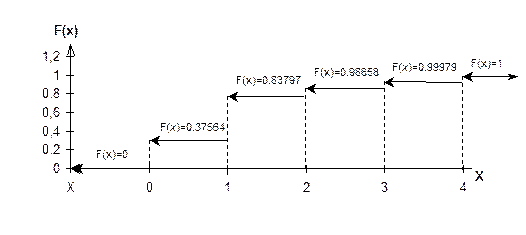
Рис. 4.9.

г) Определим вероятность того, что среди 4-х отобранных билетов окажется не меньше трех выигрышных.

“Не меньше трех” - “как минимум три” - “три или больше”. Другими словами, “не меньше трех” - это “или три, или четыре”.

Исходя из этого, для определения вероятности того, что среди отобранных 4-х билетов окажется не меньше трех выигрышных билетов, можно применить теорему сложения вероятностей несовместных событий:

P(X ³ 3) = P(X = 3) + P(X = 4) = 0,01321 + 0,00021 = 0,01342.

Вероятность того, что среди отобранных окажется не меньше трех выигрышных билетов составляет 0,01342.

д) Определим теперь вероятность того, что среди отобранных 4-х билетов окажется не больше одного выигрышного билета.

“Не больше одного” - это “один или меньше” - “или ноль, или один”.

Следовательно, для определения вероятности того, что среди отобранных окажется не больше одного выигрышного билета, также применяем теорему сложения вероятностей для несовместных событий:

P(X £ 1) = P(X = 0) + P(X = 1) = 0,37564 + 0,46233 = 0,83797.

Ответ. Р(Х 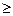3) = 0,01342; Р(Х £ 1) = 0,83797.

Задачи к теме 4

1. В городе 10 коммерческих банков. У каждого риск банкротства в течение года составляет 10%.

а) Составьте ряд распределения числа банков, которые могут обанкротиться в течение следующего года; постройте его график.

б) Найдите числовые характеристики этого распределения;

в) Запишите в общем виде функцию распределения вероятностей и постройте ее график;

г) Чему равна вероятность того, что в течение года обанкротятся не больше одного банка?

2. В лотерее на 100 билетов разыгрываются две вещи, стоимости которых 210 и 60 условных денежных единиц.

1) Составьте ряд распределения суммы выигрыша для лица, имеющего:

а) один билет;

б) два билета.

Стоимость билета - 3 условные единицы;

2) Найдите числовые характеристики этих распределений;

3) Запишите в общем виде функции распределений вероятностей и постройте их графики.

3. Нефтеразведовательная компания получила финансирование для проведения 6 нефтеразработок. Вероятность успешной нефтеразведки 0,05. Предположим, что нефтеразведки осуществляют независимые друг от друга разведывательные партии.

а) Составьте ряд распределения числа успешных нефтеразведок;

б) Найдите числовые характеристики этого распределения;

в) Запишите в общем виде функцию распределения вероятностей и постройте ее график;

г) Чему равна вероятность того, что как минимум две нефтеразведки принесут успех?

4. Под руководством бригадира производственного участка работают три мужчины и четыре женщины. Бригадиру необходимо выбрать двух рабочих для специальной работы. Не желая оказывать кому-либо предпочтения, он решил выбрать двух рабочих случайно.

а) Составьте ряд распределения числа женщин в выборке.

б) Найдите числовые характеристики этого распределения.

в) Запишите в общем виде функцию распределения вероятностей и постройте ее график;

г) Какова вероятность того, что будет выбрано не более одной женщины?

5. Некоторый ресторан славится хорошей кухней. Управляющий ресторана хвастает, что в субботний вечер в течение получаса подходит до 9 групп посетителей.

а) Составьте ряд распределения возможного числа групп посетителей ресторана в течение получаса; постройте его график.

б)Найдите числовые характеристики этого распределения;

в) Запишите в общем виде функцию распределения вероятностей и постройте ее график;

г) Чему равна вероятность того, что три или более групп посетителей прибудут в ресторан в течение 10-минутного промежутка времени?

6. Хорошим считается руководитель, принимающий не менее 70 процентов правильных решений. Такому управляющему банком предстоит принять решения по четырем важным вопросам банковской политики.

а) Считая вероятность принятия правильного решения постоянной, составьте ряд распределения возможного числа правильных решений управляющего; постройте его график.

б) Найдите числовые характеристики этого распределения;

в) Запишите в общем виде функцию распределения вероятностей и постройте ее график;

г) Чему равна вероятность того, что управляющий примет менее трех правильных решений?

7. В банк поступило 30 авизо. Подозревают, что среди них 5 фальшивых. Тщательной проверке подвергается 15 случайно выбранных авизо.

а) Составьте ряд распределения числа фальшивых авизо, которые могут быть выявлены в ходе проверки; постройте его график.

б) Найдите числовые характеристики этого распределения;

в) Запишите в общем виде функцию распределения вероятностей и постройте ее график;

г) Чему равна вероятность того, что в ходе проверки обнаружится менее двух фальшивок?

8. В течение семестра преподаватели проводят консультации по вопросам, которые остались неясными для студентов. Преподаватель, проводящий консультации по статистике, заметил, что в среднем восемь студентов посещают его за час консультационного времени, хотя точное число студентов, посещающих консультацию в определенный день, в назначенный час, - случайная величина.

а) Составьте ряд распределения числа студентов, посещающих консультации преподавателя по статистике в течение часа;

б) Найдите числовые характеристики этого распределения;

в) Запишите в общем виде функцию распределения вероятностей и постройте ее график;

г) Чему равна вероятность того, что трое студентов придут на консультацию в течение определенного получаса?

9.В ходе аудиторской проверки строительной компании аудитор случайным образом отбирает пять счетов.

а) При условии, что 3% счетов содержат ошибки, составьте ряд распределения правильных счетов;

б) Найдите числовые характеристики этого распределения;

в) Запишите в общем виде функцию распределения вероятностей и постройте ее график;

г) Чему равна вероятность того, что хотя бы один счет будет с ошибкой?

10. Записи страховой компании показали, что 30% держателей страховых полисов старше 50 лет потребовали возмещения страховых. Для проверки в случайном порядке было отобрано 15 человек старше 50 лет, имеющих полисы.

а) Составьте ряд распределения числа предъявленных претензий;

б) Найдите числовые характеристики этого распределения;

в) Запишите в общем виде функцию распределения вероятностей и постройте ее график;

г) Чему равна вероятность того, что, по крайней мере, 10 человек потребуют возмещения страховых сумм?

11. Экзаменационный тест имеет 15 вопросов, каждый из которых имеет 5 возможных ответов и только 1 из них верный. Предположим, что студент, который сдает экзамен, знает ответы не на все вопросы.)

а) Составьте ряд распределения числа правильных ответов студента на вопросы теста и постройте его график;

б) Найдите числовые характеристики этого распределения;

в) Запишите функцию распределения вероятностей и постройте ее график;

г) Чему равна вероятность того, что студент правильно ответит, по крайней мере, на 10 вопросов?

12. Для того чтобы проверить точность своих финансовых счетов, компания регулярно пользуется услугами аудиторов для проверки в бухгалтерских проводках счетов. Предположим, что служащие компании при обработке входящих счетов допускают примерно 5% ошибок. Предположим, аудитор случайно отбирает 3 входящих документа.

а) Составьте ряд распределения числа ошибок, выявленных аудитором;

б) Найдите числовые характеристики этого распределения;

в) Запишите функцию распределения вероятностей и постройте ее график;

г) Определите вероятность того, что аудитор обнаружит более чем одну ошибку.

13. В городе 10 машиностроительных предприятий, из которых 6 - рентабельных и 4 - убыточных. Программой приватизации намечено приватизировать 5 предприятий.

а) При условии проведения приватизации в случайном порядке составьте ряд распределения числа рентабельных предприятий, попавших в число приватизируемых; постройте его график.

б) Найдите числовые характеристики этого распределения;

в) Запишите функцию распределения вероятностей и постройте ее график;

г) Чему равна вероятность того, что будет приватизировано не менее четырех рентабельных предприятий?

14. В международном аэропорту время прибытия самолетов различных рейсов высвечивается на электронном табло. Появление информации о различных рейсах происходит случайно и независимо друг от друга. В среднем в аэропорт прибывает 10 рейсов в час.

а) Составьте ряд распределения числа сообщений о прибытии самолетов в течение часа;

б) Найдите числовые характеристики этого распределения;

в) Запишите функцию распределения вероятностей и постройте ее график;

г) Чему равна вероятность того, что в течение часа прибудут не менее трех рейсов?

д) Чему равна вероятность того, что в течение четверти часа не прибудет ни один самолет?

15. Телевизионный канал рекламирует новый вид детского питания. Вероятность того, что телезритель увидит эту рекламу, оценивается в 0,2. В случайном порядке выбраны 10 телезрителей.

а) Составьте ряд распределения числа лиц, видевших рекламу;

б) Найдите числовые характеристики этого распределения;

в) Запишите функцию распределения вероятностей и постройте ее график;

г) Чему равна вероятность того, что по крайней мере 2 телезрителя этого канала видели рекламу нового детского питания?

16. В течение часов-пик в общественном транспорте города происходит в среднем два дорожных происшествия в час. Утреннее время пик длится полтора часа, а вечернее - два часа.

а) Составьте ряды распределения числа дорожных происшествий в утренние и вечерние часы пик и постройте их графики;

б) Найдите числовые характеристики этих распределений;

в) Запишите функции распределений вероятностей и постройте их графики;

г) Чему равна вероятность того, что в определенный день в течение и утреннего, и вечернего времени не произойдет ни одного дорожного происшествия?

17. В магазине имеется 15 автомобилей определенной марки. Среди них - 7 автомобилей черного цвета, 6 - серого и 2 - белого. Представители фирмы обратились в магазин с предложением о продаже им трех автомобилей этой марки, безразлично какого цвета.

а) Составьте ряд распределения числа проданных автомобилей черного цвета при условии, что автомобили отбирались случайно и постройте его график;

б) Найдите числовые характеристики этого распределения;

в) Напишите функцию распределения вероятностей и постройте ее график;

г) Какова вероятность того, что среди проданных фирме автомобилей окажется, по крайней мере, 2 автомобиля черного цвета?

18. На предприятии 1000 единиц оборудования определенного вида Вероятность отказа единицы оборудования в течение часа составляет 0,001.

а) Составьте ряд распределения числа отказов оборудования в течение часа;

б) Найдите числовые характеристики этого распределения;

в) Запишите в общем виде функцию распределения вероятностей и постройте ее график;

г) Чему равна вероятность того, что в течение часа откажут как минимум 2 единицы оборудования?

19.Торговый агент в среднем контактирует с восемью потенциальными покупателями в день. Из опыта ему известно, что вероятность того, что потенциальный покупатель совершит покупку, равна 0,1.

а) Составьте ряд распределения ежедневного числа продаж для агента и постройте его график;

б) Найдите числовые характеристики этого распределения;

в) Запишите в общем виде функцию распределения вероятностей и постройте ее график;

г) Чему равна вероятность того, что у агента будут хотя бы две продажи в течение дня?

20. Прибытие посетителей в банк подчиняется одному из теоретических законов распределения. Предполагая, что в среднем в банк каждые три минуты входит один посетитель:

а) Составьте ряд распределения возможного числа посетителей банка в течение 15 минут;

б) Найдите числовые характеристики этого распределения;

в) Запишите в общем виде функцию распределения вероятностей и постройте ее график;

г) Определите вероятность того, что, по крайней мере, три посетителя войдут в банк в течение одной минуты?

5. Непрерывные случайные величины .

Дата добавления: 2014-10-22