График функции распределения вероятностей дискретной случайной величины

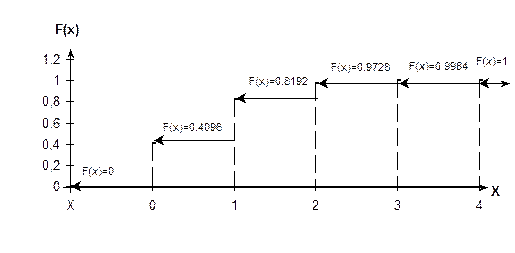
Рис. 4.4

г) Определим вероятность того, что среди 4-х случайно отобранных человек не будет ни одного человека, предпочитающего добираться на работу личным автотранспортом.

Р(Х = 0) = 0,4096.

Вероятность того, что среди 4-х случайно отобранных человек не будет ни одного, предпочитающего добираться на работу личным автотранспортом составляет 0,4096.

д) Определим вероятность того, что среди 4-х случайно отобранных человек будет хотя бы один человек, предпочитающий добираться на работу личным автотранспортом.

“Хотя бы один” - “как минимум один” - “один или больше”. Другими словами, “хотя бы один” - это “или один, или два, или три, или четыре”.

Исходя из этого, для определения вероятности того, что среди 4-х случайно отобранных человек будет хотя бы один, предпочитающий добираться на работу личным автотранспортом, можно использовать теорему сложения вероятностей несовместных событий:

P(X ³ 1) = P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4)

P(X ³ 1) = 0,4096 + 0,1536 + 0,0256 + 0,0016 = 0,5904.

С другой стороны, все возможные значения случайной величины образуют полную группу событий, а сумма их вероятностей равна 1. По отношению к событию (Х ³ 1) до полной группы событий не хватает события (Х = 0), которое является противоположным событию (Х ³ 1). Поэтому искомую вероятность того, среди 4-х случайно отобранных человек будет хотя бы один, предпочитающий добираться на работу личным автотранспортом, проще найти следующим образом:

P(X ³ 1) + P(X < 1) = 1, откуда

P(X ³ 1) = 1 - P(X = 0) = 1 - 0,4096 = 0,5904.

Вероятность того, что среди 4-х случайно отобранных человек будет хотя бы один человек, предпочитающий добираться на работу личным автотранспортом, составляет 0,5904.

е) Определим вероятность того, что среди 4-х случайно отобранных человек будет не больше двух, предпочитающих добираться на работу личным автотранспортом.

“Не больше двух” - “два или меньше”, т.е. “или ноль, или один, или два”.

Используем теорему сложения вероятностей несовместных событий:

P(X £ 2) = P(X = 0) + P(X = 1) + P(X = 2)

P(X £ 2) = 0,4096 + 0,4096 + 0,1536 = 0,9728.

Вероятность того, что среди 4-х случайно отобранных человекбудет не больше двух, предпочитающих добираться на работу личным автотранспортом, составляет 0,9728.

Пример 4.2 Среднее число инкассаторов, прибывающих утром на автомобиле в банк в 15-ти минутный интервал, равно 2. Прибытие инкассаторов происходит случайно и независимо друг от друга.

а) Составьте ряд распределения числа инкассаторов, прибывающих утром на автомобиле в банк в течение 15-ти минут;

б) Найдите числовые характеристики этого распределения;

в) Напишите функцию распределения числа инкассаторов, прибывающих утром на автомобиле в банк в течение 15-ти минут, и постройте её график;

г) Определите, чему равна вероятность того, что в течение 15 минут в банк прибудут на автомобиле хотя бы два инкассатора;

д) Определите вероятность того, что в течение 15 минут число прибывших инкассаторов окажется меньше трех.

Решение. Пусть случайная величина Х - число инкассаторов, прибывающих утром на автомобиле в банк в течение 15-ти минут. Перечислим все возможные значения случайной величины Х: 0, 1, 2, 3, 4, 5,..., n.

Это - дискретная случайная величина, т.к. ее возможные значения отличаются друг от друга не менее чем на 1, и множество ее возможных значений является счетным.

По условию прибытие инкассаторов происходит случайно и независимо друг от друга. Следовательно, мы имеем дело с независимыми испытаниями.

Если мы предположим, что вероятность прибытия инкассаторов на автомобиле одинакова в любые два периода времени равной длины, и что прибытие или неприбытие автомобиля в любой период времени не зависит от прибытия или неприбытия в любой другой период времени, то последовательность прибытия инкассаторов в банк может быть описана распределением Пуассона.

Итак, случайная величина Х - число инкассаторов, прибывающих утром на автомобиле в течение 15-ти минут, подчиняется распределению Пуассона. По условию задачи: l = np = 2; X = m.

а) Составим ряд распределения.

Вычислим вероятности того, что случайная величина примет каждое из своих возможных значений и запишем полученные результаты в таблицу.

Так как данная случайная величина Х подчинена распределению Пуассона, расчет искомых вероятностей осуществляется по формуле Пуассона (4.13).

Найдем по этой формуле вероятность того, что в течение 15-ти минут утром на автомобиле прибудет 0 инкассаторов:

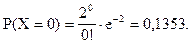
Однако, расчет вероятностей распределения Пуассона легче осуществлять, пользуясь специальными таблицами вероятностей распределения Пуассона. В этих таблицах содержатся значения вероятностей при заданных m и (см. Приложение 6).

По условию l = 2, а m изменяется от 0 до n.

Воспользовавшись таблицей распределения Пуассона, получим:

Р(Х = 0) = 0,1353; Р(Х = 1) = 0,2707;

Р(Х = 2) = 0,2707; Р(Х = 3) = 0,1804;

Р(Х = 4) = 0,0902; Р(Х = 5) = 0,0361;

Р(Х = 6) = 0,0120; Р(Х = 7) = 0,0034;

Р(Х = 8) = 0,0009; Р(Х = 9) = 0,0002.

Данных для l = 2, и m > = 10 в таблице нет, что указывает на то, что эти вероятности составляют менее 0, 0001, т.е.

Р(Х = 10)» 0. Понятно, что Р(Х = 11) еще меньше отличается от 0.

Занесем полученные результаты в таблицу:

X
Р(Х)	0,1353	0,2707	0,2707	0,1804	0,0902	0,0361	0,0120	0,0034	0,0009	0,0002	0,0000

Так как все возможные значения случайной величины образуют полную группу событий, сумма их вероятностей должна быть равна 1.

Проверим: 0,1353 + 0,2707 + 0,2707 + 0,1804 + 0,0902 + 0,0361 + 0,0120 +

+ 0,0034 + 0,0009 + 0,0002 = 0,9999» 1.

График, полученного ряда распределения дискретной случайной величины Х – полигон распределения вероятностей:

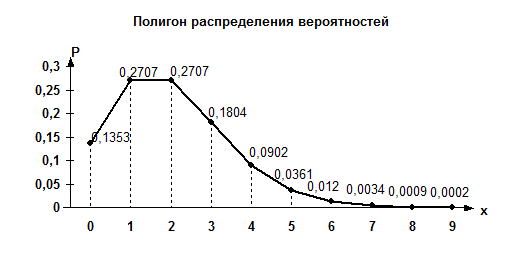
Рис. 4.5.

б) Найдем основные числовые характеристики полученного распределения случайной величины Х.

Можно рассчитать математическое ожидание, дисперсию и среднее квадратическое отклонение по общим для любой дискретной случайной величины формулам.

Математическое ожидание случайной величины, подчиняющейся распределению Пуассона, может быть рассчитано и по формуле(4.13.):

M(X = m) = n × p = l.

M(X = m) = l = 2 (инкассатора).

Для выполнения дисперсии случайной величины, подчиняющейся распределению Пуассона, можно применить формулу:

D(X = m)»l.

Итак, дисперсия числа инкассаторов, прибывающих утром на автомобиле в течение 15-ти минут:

D(X = m) = l = 2 (кв.ед.)

Среднее квадратическое отклонение числа инкассаторов, прибывающих утром на автомобиле в течение 15-ти минут:

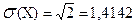(инкассатора).

в)Зададим теперь дискретную случайную величину в виде функции распределения:

Дата добавления: 2014-10-22