
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Необходимо определить вероятность события А и переоценить вероятности событий Hi с учетом полной информации о событии А
|
|
|
|
БАЙЕСА
ФОРМУЛЫ ПОЛНОЙ ВЕРОЯТНОСТИ И
Часто мы начинаем анализ вероятностей имея предварительные, априорные значения вероятностей интересующих нас событий. Затем из источников информации, таких как выборка, отчет, опыт и т.д. мы получаем дополнительную информацию об интересующем нас событии. Имея эту новую информацию, мы можем уточнить, пересчитать значения априорных вероятностей. Новые значения вероятностей для тех же интересующих нас событий будут уже апостериорными ( послеопытными) вероятностями. Теорема Байеса дает нам правило для вычисления таких вероятностей.
Последовательность процесса переоценки вероятностей можно схематично изобразить так:





 Априорные Новая информация из Байесовский Апостериорные
Априорные Новая информация из Байесовский Апостериорные
вероятности каких-либо источников анализ вероятности
Пусть событие А может осуществиться лишь вместе с одним из событий Н1, Н2, Н3,..., Нn, образующих полную группу. Пусть известны вероятности P(H1), P(H2),…P(Hi),…P(Hn). Так как события Hi образуют полную группу, то  . Так же известны и условные вероятности события А: P(A/H1), P(A/H2), …P(A/Hi)…, P(A/Hn), i=1, 2, …, n. Так как заранее неизвестно с каким из событий Hi произойдет событие А, то события Hi называют гипотезами.
. Так же известны и условные вероятности события А: P(A/H1), P(A/H2), …P(A/Hi)…, P(A/Hn), i=1, 2, …, n. Так как заранее неизвестно с каким из событий Hi произойдет событие А, то события Hi называют гипотезами.
Вероятность события А определяется как:
 (3.1)
(3.1)
Эта вероятность называется полной вероятностью.
Если событие А может наступить только вместе с одним из событий Н1, Н2, Н3,..., Нn, образующих полную группу несовместных событий и называемых гипотезами, то вероятность события А равна сумме произведений вероятностей каждого из событий Н1, Н2,..., Нn на соответствующую условную вероятность события А.
Условные вероятности гипотез вычисляются по формуле:

или (3.2)

Это - формулы Байеса, (по имени английского математика Т.Байеса, опубликовавшего их в 1764 году) выражение в знаменателе - формула полной вероятности.
Пример 3.1. Предприятие, производящее компьютеры, получает одинаковые ЧИПы от двух поставщиков. Первый поставляет 65% ЧИПов, второй 35%. Известно, что качество поставляемых ЧИПов разное. Основываясь на предыдущих данных о рейтингах качества, составлена следующая таблица:
| Поставщик | % качественной продукции | % брака |
| Поставщик 1 | ||
| Поставщик 2 |
Предприятие осуществляет гарантийный ремонт компьютеров. Имея данные о числе компьютеров, поступающих на гарантийный ремонт в связи с неисправностью ЧИПов, переоцените вероятности того, что возвращенный для ремонта компьютер, укомплектован ЧИПом от поставщика 1, поставщика 2.
Решение задач с использованием формул полной вероятности и Байеса удобнее оформлять в виде таблицы следующего вида:
Гипотезы
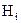
| Априорные
вероятности

| Условные вероятности

| Совместные
вероятности
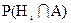
| Апостериорные вероятности P(Hi /A) |
Шаг 1. В первой колонке перечисляем события, которые задают априорную информацию в контексте решаемой проблемы.
Соб. Н1 - ЧИП от первого поставщика;
Соб. Н2 - ЧИП от второго поставщика.
Это - гипотезы и они образуют полную группу независимых и несовместных событий.
Во второй колонке записываем вероятности этих событий:
Р(Н1) = 0,65, а Р(Н2) = 0,35
В третьей колонке определим условные вероятности события А - «ЧИП бракованный» для каждой из гипотез.
Шаг 2. В колонке 4 находим вероятности для событий «ЧИП от первого поставщика и он бракованный» и «ЧИП от второго поставщика и он бракованный». Они определяются по правилу умножения вероятностей путем перемножения значений колонок 2 и 3. Поскольку сформулированные события являются результатом пересечения двух событий: А и Hi, то их называют совместными вероятностями, то есть 
Шаг 3. Суммируем вероятности в колонке 4 для того, чтобы найти вероятность события А. В нашем примере 0,0130 - вероятность поставки некачественного ЧИПа от поставщика1, 0,0175 - вероятность поставки некачественного ЧИПа от поставщика 2. Поскольку, как мы уже сказали выше, ЧИПы поступают только от двух поставщиков, то сумма вероятностей 0,0130 и 0,0175 показывает, что 0,0305 есть вероятность бракованного ЧИПа в общей поставке, по формуле (3.1):
 = 0,0130 + 0,0175 = 0,0305
= 0,0130 + 0,0175 = 0,0305
Шаг 4. В колонке 5 вычисляем апостериорные вероятности, используя формулу (3.2)

Заметим, что совместные вероятности находятся в строках колонки 4, а вероятность события А как сумма колонки 4.
Гипотезы
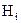
| Априорные
вероятности

| Условные вероятности

| Совместные
вероятности
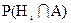
| Апостериорные вероятности

|
| ЧИП от 1-го поставщика ЧИП от 2-го поставщика | 0,65 0,35 | 0,02 0,05 | 0,0130 0,0175 | 0,426 0,574 |
| S | - | Р(А) = 0,305 |
Пример 3.2. Экономист полагает, что вероятность роста стоимости акций некоторой компании в следующем году равна 0,75, если экономика страны будет на подъёме; и эта же вероятность равна 0,30, если экономика страны не будет успешно развиваться. По его мнению, вероятность экономического подъёма в будущем году равна 0,80. Используя предположения экономиста, оцените вероятность того, что акции компании поднимутся в цене в следующем году?
Решение. Определим события:
А - “акции компании поднимутся в цене в будущем году”.
Событие А - “акции компании поднимутся в цене в будущем году” - может произойти только вместе с одной из гипотез:
Н1 - экономика страны будет на подъёме и
Н2 - экономика страны не будет успешно развиваться.
По условию известны вероятности гипотез:
P(H1) = 0,8; P(H2) = 0,2
и условные вероятности события А:
P(A/H1) = 0,75; P(A/H2) = 0,3.
Гипотезы образуют полную группу, сумма их вероятностей равна 1. Рассмотрим событие А - это (или Н1А или Н2А). События Н1А и Н2А - несовместные попарно, так как события Н1 и Н2 - несовместны.
События Н1 и А, Н2 и А - зависимые.
Вышеизложенное позволяет применить для определения искомой вероятности события А формулу полной вероятности:
P(A)=P(H1) × P(A/H1) + P(H2) × P(A/H2) = 0,8 × 0,75 + 0,2 × 0,3 = 0,66.
Оформим решение в рабочей таблице:
| Гипотезы Hi | P(Hi) | P(A/Hi) | P(Hi)· P(A/Hi) |
| H1 - “подъем экономики” | 0,80 | 0,75 | 0,60 |
| H2- “спад экономики” | 0,20 | 0,30 | 0,06 |
| S | 1,00 | - | 0,66 |
Ответ. Вероятность того, что акции компании поднимутся в цене в следующем году,
составляет 0,66.
Пример 3.3. Экономист полагает, что в течение периода активного экономического роста американский доллар будет расти в цене с вероятностью 0,7, в период умеренного экономического роста доллар подорожает с вероятностью 0,4 и при низких темпах экономического роста доллар подорожает с вероятностью 0,2. В течение любого периода времени вероятность активного экономического роста 0,3, умеренного экономического роста 0,5 и низкого роста - 0,2. Предположим, что доллар дорожает в течение текущего периода. Чему равна вероятность того, что анализируемый период совпал с периодом активного экономического роста?
Решение. Определим события:
А - “доллар дорожает”. Оно может произойти только вместе с одной из гипотез:
Н1 - “активный экономический рост”;
Н2 - “умеренный экономический рост”;
Н3 - “низкий экономический рост”.
По условию известны доопытные (априорные) вероятности гипотез и условные вероятности события А:
Р(Н1) = 0,3; Р(Н2) = 0,5; Р(Н3) = 0,2;
Р(А/Н1) = 0,7; Р(А/Н2) = 0,4 и Р(А/Н3) = 0,2.
Гипотезы образуют полную группу, сумма их вероятностей равна 1. Событие А - это (или Н1 × А или Н2 × А или Н3 × А). События Н1 × А, Н2 × А и Н3 × А - несовместные попарно, так как события Н1, Н2 и Н3 - несовместны.
События Н1 и А, Н2 и А, Н3 и А - зависимые.
По условию требуется найти уточненную (послеопытную, апостериорную) вероятность первой гипотезы, т.е. необходимо найти вероятность активного экономического роста, при условии, что доллар дорожает (событие А уже произошло), то есть Р(Н1/А) -?
Используя формулу Байеса (3.2) и подставляя заданные значения вероятностей, имеем:

Мы можем получить тот же результат при помощи таблицы:
| Гипотезы Hi | Априорные вероятности P(Hi) | Условные вероятности P(A/Hi) | Совместные
вероятности
P(A Hi) Hi)
| Апостериорные вероятности P(Hi/A) |
| H1 | 0,30 | 0,70 | 0,21 | 0,21 / 0,45 = 0,467 |
| H2 | 0,50 | 0,40 | 0,20 | 0,20 / 0,45 = 0,444 |
| H3 | 0,20 | 0,20 | 0,04 | 0,04 / 0,45 = 0,089 |
| S | 1,00 | - | 0,45 |
Ответ. Вероятность активного экономического роста, при условии, что доллар дорожает, составляет 0,467.
Для более наглядного восприятия решения нашей задачи мы можем также построить дерево решений:
| Совместные | ||
| Априорные | Условные | вероятности |
| вероятности | вероятности | (как произведение) |

| P(A/H1) = 0,7 |  P(H1A) = 0,3× 0,7 = 0,21 P(H1A) = 0,3× 0,7 = 0,21
|
| Р(Н1) = 0,3 | ||
P(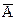 /H1) = 0,3 /H1) = 0,3
| P(H1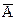 ) = 0,3× 0,3 = 0,09 ) = 0,3× 0,3 = 0,09
| |
| Р(Н2) = 0,5 | P(A/H2) = 0,4 | P(H2A) = 0,5× 0,4 = 0,20 |
P(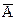 /H2) = 0,6 /H2) = 0,6
| P(H2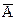 ) = 0,5× 0,6 = 0,30 ) = 0,5× 0,6 = 0,30
| |
| P(A/H3) = 0,2 | P(H3A) = 0,2 × 0,2 = 0,04 | |
| Р(Н3) = 0,2 | ||
P(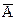 /H3) = 0,8 /H3) = 0,8
| P(H3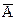 ) = 0,2× 0,8 = 0,16 ) = 0,2× 0,8 = 0,16
|
Ответ. Вероятность активного экономического роста при условии, что доллар подорожает,
P(Hi/A) =0,467
Пример 3.3. В каждой из двух урн содержится 6 черных и 4 белых шара. Из первой урны во вторую наудачу переложен один шар.
1. Найти вероятность того, что шар, извлеченный из второй урны после перекладывания, окажется черным?
2. Предположим, что шар, извлеченный из второй урны после перекладывания, оказался черным. Какова тогда вероятность того, что из первой урны во вторую был переложен белый шар?
Решение. Определим события:
А - “шар, извлеченный из второй урны - черный”. Оно может произойти только вместе с одной из гипотез:
Н1 - “из 1-й урны во 2-ю урну переложили черный шар” и
Н2 - “из 1-й урны во 2-ю урну переложили белый шар”.
Используя классическое определение вероятностей, определим вероятности гипотез:
P(H1) = 6/10; P(H2) = 4/10.
и условные вероятности события А.
После перекладывания во второй урне окажется 11 шаров. Если из первой урны во вторую переложили черный шар, то во второй урне окажется 7 черных и 4 белых шаров.
Тогда P(A/H1) = 7/11.
Если из первой урны во вторую переложили белый шар, то во второй урне окажется 6 черных и 5 белых шаров.
Тогда P(A/H2) = 6/11.
Гипотезы образуют полную группу, сумма их вероятностей равна 1. Рассмотрим событие А - это (или Н1А или Н2А). События Н1А и Н2А - несовместные попарно, так как события Н1 и Н2 - несовместны.
События Н1 и А, Н2 и А - зависимые.
1. Вышеизложенное позволяет применить для определения вероятности события А и ответа на первый вопрос формулу полной вероятности (3.1):
P(A)=P(H1)P(A/H1) + P(H2)P(A/H2)=6/10 7/11 + 4/106/11 = 0,6.
Это же решение можно оформить в рабочей таблице:
| Гипотезы Hi | P(Hi) | P(A/Hi) | P(Hi) P(A/Hi) |
| H1 - “из 1-й урны во 2-ю урну переложили черный шар” | 6/10 | 7/11 | 42/110 |
| H2- “из 1-й урны во 2-ю урну переложили белый шар” | 4/10 | 6/11 | 24/110 |
| S | 1,00 | - | 0,6 |
Ответ. Вероятность того, что шар, извлеченный из второй урны после перекладывания, окажется черным составляет 0,6.
2. Во второй части задачи предполагается, что событие А уже произошло, т.е. шар, извлеченный из второй урны, оказался черным. Требуется найти уточненную (послеопытную, апостериорную) вероятность второй гипотезы, т.е. необходимо найти вероятность того, что из первой урны во вторую был переложен белый шар при условии, что шар, извлеченный из второй урны после перекладывания, оказался черным.
Р(Н2/А) -?
Для определения искомой вероятности воспользуемся формулой Байеса (3.2):

Мы можем получить тот же результат при помощи таблицы:
| Гипотезы Hi | Априорные вероятности P(Hi) | Условные вероятности P(A/Hi) | Совместные
вероятности
P(A Hi) Hi)
| Апостериорные вероятности P(Hi/A) |
| H1 | 6/10 | 7/11 | 42/110=0,3818 | 0,3818/0,6 = 0,6364 |
| H2 | 4/10 | 6/11 | 24/110=0,2182 | 0,2182/0,6 = 0,3636 |
| S | 1,00 | - | 0,6 |
Ответ. Вероятность того, что из первой урны во вторую был переложен белый шар при условии, что шар, извлеченный из второй урны после перекладывания, оказался черным, составляет 0,3636.
|
|
|
|
|
Дата добавления: 2014-10-22; Просмотров: 1071; Нарушение авторских прав?; Мы поможем в написании вашей работы!