Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий

Для несовместных событий A, B:
или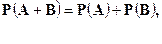	(2.5)

Правило сложения вероятностей справедливо и для конечного числа n попарно несовместных событий, то есть:

P(A₁+A₂+A₃+...+A_n)=P(A₁)+P(A₂)+P(A₃)+...P(A_n )

или

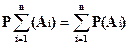
(2.6)

В случае нескольких совместных событий необходимо по аналогии с рассуждениями о пересечении двух совместных событий исключить повторный учет областей пересечения событий. Рассмотрим три совместных события.

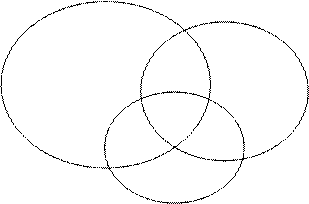A	AB	B
	ABC
AC	C	CB

Рис. 2.3

Для случая трех совместных событий можно записать:

Р(А + В + С) = Р(А) + Р(В) + Р(С) - Р(АВ) - Р(АС) - Р(ВС) + Р(АВС).

Сумма вероятностей событий А₁, А₂, А₃,..., А_n, образующих полную группу, равна 1, то есть:

P(A₁) + P(A₂) + P(A₃) +... + P(A_n) = 1

или

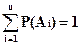
(2.7)

Пример 2.3 Компания производит 40000 холодильников в год, которые реализуются в различных регионах России. Из них 10000 экспортируются в страны СНГ, 8000 продаются в регионах Европейской части России, 7000 продаются в страны дальнего зарубежья, 6000 в Западной Сибири, 5000 в Восточной Сибири, 4000 в Дальневосточном районе. Чему равна вероятность того, что определенный холодильник будет: 1. Произведен на экспорт? 2. Продан в России?

Решение. Обозначим события:

А – «Холодильник будет продан в странах СНГ»,

В – «Холодильник будет продан в Европейской части России»,

С – «Холодильник будет продан в страны дальнего зарубежья»,

D – «Холодильник будет продан в Западной Сибири»,

E – «Холодильник будет продан в Восточной Сибири»,

F – «Холодильник будет продан в Дальневосточном районе».

Соответственно,

Вероятность того, что холодильник будет продан в странах СНГ:

P(A) = 10000/40000 =0,25.

Вероятность того, что холодильник будет продан в Европейской части России:

P(B) = 8000/40000 = 0,20.

Вероятность того, что холодильник будет продан в страны дальнего зарубежья:

P(C) = 7000/40000 = 0,175.

Вероятность того, что холодильник будет продан в Западной Сибири:

P(D) = 6000/40000 = 0,15.

Вероятность того, что холодильник будет продан в Восточной Сибири:

P(E) = 5000/40000 = 0,125.

Вероятность того, что холодильник будет продан на Дальнем Востоке:

P(F) = 4000/40000 = 0,10.

События А, B, C, D, E, F – несовместные.

1.Событие, состоящее в том, что холодильник произведен на экспорт, означает, что холодильник будет продан или в страны СНГ, или страны дальнего зарубежья. Отсюда, по формуле (2.5) находим его вероятность: P(холодильник произведен на экспорт) = P(A + B) = Р(А) + Р(B) = 0,25 + 0,175 = 0,425.

2. Событие, состоящее в том, что холодильник будет продан в России, означает, что холодильник будет продан или в Европейской части России, или в Западной Сибири, или в Восточной Сибири, или на Дальнем Востоке. Отсюда, по формуле (2.6) находим его вероятность:

Р(холодильник будет продан в России) = P(A + D + E + F) = P(B) + P(D) + P(E) + P(F) = 0,20 + 0,15 + 0,125 + 0,10 = 0,575.

Этот же результат можно было получить рассуждая по другому. События «Холодильник произведен на экспорт» и «Холодильник будет продан в России» – два взаимно противоположных события, отсюда по формуле (2. 3):

Р(холодильник будет продан в России) = 1 - P(холодильник произведен на экспорт) = 1 – 0,425 =

= 0,575.

Ответ: 1. P(холодильник произведен на экспорт) = 0,425, 2. Р(холодильник будет продан в России) == 0,575.

Пример 2.4 Опыт состоит в случайном извлечении карты из колоды в 52 карты. Чему равна вероятность того, что это будет или туз, или карта масти треф?

Решение. Определим события: А - “извлечение туза”, В - “извлечение карты трефовой масти”. Вероятность извлечения туза из колоды карт Р(А) = 4/52; вероятность извлечения карты трефовой масти - Р(В) = 13/52; вероятность их пересечения - извлечение трефового туза – P(AB) = 1/52.

Проиллюстрируем это на рисунке.

Событие А	Трефы	Бубны	Пики	Червы
	Туз	Туз	Туз	Туз
	Король	Король	Король	Король
	Дама	Дама	Дама	Дама
Событие	Валет	Валет	Валет	Валет
В
	...	...	...	...

Рис. 2.4

События А и В - совместные, поскольку в колоде есть трефовый туз.

Согласно условию задачи, нас интересует вероятность суммы совместных событий А и В. По формуле 2.4 получим:

P(A + B) = P(A) + P(B) – P (AB) = 4/52 + 13/52 - 1/52 = 16/52 = 0,3077

Ответ: Вероятность того, что случайно выбранная карта будет или туз, или масти трефа равна 0,3077.

Пример 2.5. В урне два белых и три черных шара. Чему равна вероятность появления белого шара при первом извлечении из урны? При втором извлечении из урны?

Решение. Здесь возможны два случая.

Первый случай. Схема возвращенного шара, то есть шар после первого испытания возвращается в урну.

Пусть событие А - “появление белого шара при первом испытании”. Так как N = 5, а М = 2, то Р(А) = 2/5.

Пусть событие В - “появление белого шара при втором испытании”. Так как шар после первого испытания возвратился в урну, то N = 5, а М = 2 и Р(В) = 2/5.

Таким образом, вероятность каждого из событий не зависит от того, произошло или не произошло другое событие. События А и В в этом случае называются независимыми.

Итак, события А и В называются независимыми, если вероятность каждого из них не зависит от того, произошло или нет другое событие.

Вероятности независимых событий называются безусловными.

Второй случай. Схема невозвращенного шара, то есть шар после первого испытания в урну не возвращается.

Вероятность появления белого шара при первом испытании Р(А) = 2/5. Белый шар в урну не возвращается, следовательно, в урне остались один белый и три черных шара. Чему равна вероятность события В при условии, что событие А произошло? N = 4, M = 1.

Искомую вероятность обозначают Р(В/А) или Р(В)_А или Р_А(В). Итак, Р(В/А)=1/4 называют условной вероятностью, а события А, В называются зависимыми. В предыдущем примере с картами Р(А)=4/52; Р(А/В)=4/16.

Например, тот факт, что человек работает научным сотрудником, может быть является зависимыми от наличия у него высшего образования; событие, состоящее в том, что станок может выйти из строя, не является независимым от срока его эксплуатации, событие, состоящее в том, что цена акций компании пошла вверх, не является независимым от того с прибылью или с убытком сработала компания в прошлом периоде и т.д.

Итак, события А и В называются зависимыми, если вероятность каждого из них зависит от того произошло или нет другое событие. Вероятность события В, вычисленная в предположении, что другое событие А уже осуществилось, называется условной вероятностью.

Вероятность произведения двух независимых событий А и В равна произведению их вероятностей:

P(AB) = P(A) × P(B),
P(A B) = P(A) × P(B)	(2.8)

или

События А₁, А₂,..., A_n (n > 2) называются независимыми в совокупности, если вероятность каждого из них не зависит от того, произошли или нет любые события из числа остальных.

Распространим теоремы умножения на случаи n независимых и зависимых в совокупности событий.

Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий.

P(A₁ ×A₂ × A₃ ×…× A_n) = P(A₁) × P(A₂) × P(A₃) ×…× P(A_n) (2.9)

Вероятность произведения двух зависимых событий А и В равна произведению вероятности одного из них на условную вероятность другого:

	Р(АВ) = P(B) × Р(А/В)	(2.10)
	Р(АВ) = P(B) × Р(А/В)
	или Р(АВ) = P(A)×Р(В/А)
	Р(АВ) = Р(A)×(В/А)
Вероятность события В при условии появления события А:
P(B/A) =	(2.11)
.

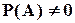Вероятность совместного наступления конечного числа n зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем условная вероятность каждого последующего события вычисляется в предположении, что все предыдущие уже наступили, т.е.

P(A1 × A2 × A3 ×... ×Аn) = Р(A1) × P(A2 / A1) ×P(A3 / A1 × A2).×... ×P(An / A1 × A2 × A3 ×…× An-1) (2.12)

Если события А₁, А₂,... A_n - зависимые в совокупности, то вероятность наступления хотя бы одного из них соответственно равна:

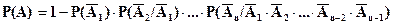(2.13)

Вероятность появления хотя бы одного события из n независимых в совокупности, равна разности между 1 и произведением вероятностей событий, противоположных данным, то есть:

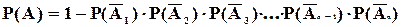(2.14)

Пример 2.6. Консультационная фирма претендует на два заказа от двух крупных корпораций. Эксперты фирмы считают, что вероятность получения консультационной работы в корпорации А равна 0,45. Эксперты также полагают, что если фирма получит заказ у корпорации А, то вероятность того, что и корпорация В обратится к ним, равна 0,9. Какова вероятность того, что консультационная фирма получит оба заказа?

Решение. Обозначим события:

А - “получение консультационной работы в корпорации А”,

В - “получение консультационной работы в корпорации В”.

События А и В - зависимые, т.к. событие В зависит от того, произойдет или нет событие А.

По условию мы имеем: Р(А) = 0,45, а также знаем, что Р(В/А) = 0,9.

Необходимо найти вероятность того, что оба события (и событие А, и событие В) произойдут, т.е. Р(АВ). Для этого используем правило умножения вероятностей (формула 2.10).

Отсюда получим:

Р(А В) = Р(А) Р(В/А) = 0,45 0,9 = 0,405.

Ответ. Вероятность того, что фирма получит оба заказа 0,405.

Пример 2.7. В большой рекламной фирме 21% работников получают высокую заработную плату. Известно также, что 40% работников фирмы - женщины, а 6,4% работников - женщины, получающие высокую заработную плату. Можем ли мы утверждать, что на фирме существует дискриминация женщин в оплате труда?

Решение. Сформулируем условие этой задачи в терминах теории вероятностей. Для ее решения необходимо ответить на вопрос: “Чему равняется вероятность того, что случайно выбранный работник будет женщиной, имеющей высокую заработную плату?” и сравнить ее с вероятностью того, что наудачу выбранный работник любого пола имеет высокую зарплату.

Обозначим события:

А - “случайно выбранный работник имеет высокую зарплату”;

В - “случайно выбранный работник - женщина”.

События А и В - зависимые.

По условию: Р(АB) = 0,064; Р(В) = 0,4; Р(А) = 0,21.

Нас интересует вероятность того, что наудачу выбранный работник имеет высокую зарплату при условии, что это женщина, т.е. - условная вероятность события А.

Тогда, используя теорему умножения вероятностей, получим:

.

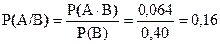Поскольку Р(А/В)=0,16 меньше, чем Р(А)=0,21, то мы можем заключить, что женщины, работающие в рекламной фирме, имеют меньше шансов получить высокую заработную плату по сравнению с мужчинами.

Ответ. На фирме существует дискриминация женщин в оплате труда.

Пример 2.8. Студент пришел на экзамен, изучив только 20 из 25 вопросов программы. Экзаменатор задал студенту три вопроса. Вычислить вероятность того, что студент ответит:

1. на все три вопроса;

2. хотя бы на один вопрос.

Решение. Обозначим события:

А -“студент знает все три вопроса”;

А₁ - “студент знает первый вопрос”;

А₂ - “студент знает второй вопрос”;

А₃ - “студент знает третий вопрос”.

По условию: P(A₁) = 20/25; P(A₂/A₁) = 19/24; P(A₃/A₂ ×A₁) = 18/23.

1. Искомое событие А состоит в совместном наступлении событий А₁, А₂, А₃.

События А₁, А₂, А₃ - зависимые.

Для решения задачи используем правило умножения вероятностей конечного числа n зависимых событий.

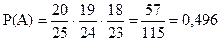
Вероятность того, что студент ответит на все три вопроса, равна 0,496.

2. Обозначим событие:

В -“студент ответит хотя бы на один вопрос”;

Событие В состоит в том, что произойдет или событие А₁, а события А₂ и А₃ - не произойдут, или произойдет событие А₂, а события А₁ и А₃ - не произойдут, или произойдет событие А₃, а события А₁ и А₂ - не произойдут, или произойдут события А₁ и А₂, а событие А₃ - не произойдет, или произойдут события А₁ и А₃, а событие А₂ - не произойдет, или произойдут события А₂ и А₃, а событие А₁ - не произойдет, или произойдут все три события А₁, А₂, А₃.

Для решения этой задачи можно было бы использовать правила сложения и умножения вероятностей. Однако здесь проще применить правило для вероятности наступления хотя бы одного из n зависимых событий:

Учитывая, что:

;

,

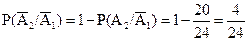получим:

.

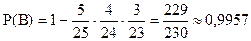Вероятность того, что студент ответит хотя бы на один вопрос, равна 0,9957.

Ответ. Вероятность того, что студент ответит на все три вопроса равна 0,496.

Вероятность того, что студент ответит хотя бы на один вопрос, равна 0,9957.

Пример 2.9. Вероятность того, что потребитель увидит рекламу определенного продукта по телевидению, равна 0,04. Вероятность того, что потребитель увидит рекламу того же продукта на рекламном стенде, равна 0,06. Предполагается, что оба события - независимы. Чему равна вероятность того, что потребитель увидит: 1. обе рекламы; 2. хотя бы одну рекламу?

Решение. Обозначим события:

А -“ потребитель увидит рекламу по телевидению”;

В - “потребитель увидит рекламу на стенде”.

С - “потребитель увидит хотя бы одну рекламу”. Это значит, что потребитель увидит рекламу по телевидению, или на стенде, или по телевидению и на стенде.

По условию: P(A) = 0,04; P(В) = 0,06.

События А и В - совместные и независимые.

1. Поскольку вероятность искомого события есть вероятность совместного наступления независимых событий A и B (потребитель увидит рекламу и по телевидению и на стенде), т.е. их пересечения, для решения задачи используем правило умножения вероятностей для независимых событий.

Отсюда:

Р(АВ) = Р(А) × Р(В) = 0,04 × 0,06 = 0,0024.

Вероятность того, что потребитель увидит обе рекламы, равна 0,0024.

2.Так как событие С состоит в совместном наступлении событий А и В, искомая вероятность может быть найдена с помощью правила сложения вероятностей.

Р(С) = Р(А + В)= Р(А) + Р(В) - Р(АВ) = 0,04 + 0,06 - 0,0024 = 0,0976.

Вместе с тем, при решении этой задачи может быть использовано правило о вероятности наступления хотя бы одного из n независимых событий:

Учитывая, что

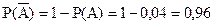и

,

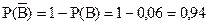получим: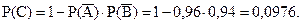

Вычисление вероятностей событий такого типа характеризует эффективность рекламы, поскольку эта вероятность может означать долю (процент) населения, охватываемого, и отсюда следует оценка рекламных усилий.

Ответ. Вероятность того, что потребитель увидит обе рекламы равна 0,024.

Вероятность того, что потребитель увидит хотя бы одну рекламу равна 0,0976.

Дата добавления: 2014-10-22