Критические точки распределения Фишера-Снедекора

(К₁ - число степеней свободы большей дисперсии,

К₂ - число степеней свободы меньшей дисперсии)

Уровень значимости a = 0,01
К₁ К₂

	98,49	99,01	90,17	99,25	99,33	99,30	99,34	99,36	99,36	99,40	99,41	99,42
	34,12	38,81	29,46	28,71	28,24	27,91	27,67	27,49	27,34	27,23	27,13	27,05
	21,20	18,00	16,69	15,98	15,52	15,21	14,96	14,80	14,66	14,54	14,45	14,37
	16,26	13,27	12,06	11,39	10,97	10,67	10,45	10,27	10,15	10,05	9,96	9,89
	13,74	10,92	9,78	9,15	8,75	8,47	8,26	8,10	7,98	7,87	7,79	7,72
	12,25	9,55	8,45	7,85	7,46	7,19	7,00	6,84	6,71	6,62	6,54	6,47
	11,26	8,65	7,59	7,01	6,63	6,37	6,19	6,03	5,91	5,82	5,74	5,67
	10,56	8,02	6,99	6,42	6,06	5,80	5,62	5,47	5,35	5,26	5,18	5,11
	10,04	7,56	6,55	5,99	5,64	5,39	5,21	5,06	4,95	4,85	4,78	4,71
	9,86	7,20	6,22	5,67	5,32	5,07	4,88	4,72	4,63	4,54	4,46	4,40
	9,33	6,93	5,95	5,41	5,06	4,82	4,65	4,50	4,39	4,30	4,22	4,16
	9,07	6,70	5,74	5,20	4,86	4,62	4,44	4,30	4,19	4,10	4,02	3,96
	8,86	6,51	5,56	5,03	4,69	4,46	4,28	4,14	4,03	3,94	3,86	3,80
	8,68	6,36	5,42	4,89	4,56	4,32	4,14	4,00	3,89	3,80	3,73	3,67
	8,53	6,23	5,29	4,77	4,44	4,20	4,03	3,89	3,78	3,69	3,61	3,55
	8,40	6,11	5,18	4,67	4,44	4,10	3,93	3,79	3,68	3,59	3,52	3,45

Уровень значимости a = 0,05
К₁ К₂

	18,51	19,00	19,16	19,25	19,30	19,33	19,36	19,37	19,38	19,39	19,40	19,41
	10,13	9,55	9,28	9,12	9,01	8,94	8,88	8,84	8,81	8,78	8,76	8,74
	7,71	6,94	6,59	6,39	6,26	6,16	6,09	6,04	6,00	5,96	5,93	5,91
	6,61	5,79	5,41	5,19	5,05	4,95	4,88	4,82	4,78	4,74	4,70	4,68
	5,99	5,14	4,76	4,53	4,39	4,28	4,21	4,15	4,10	4,06	4,03	4,00
	5,59	4,74	4,35	4,12	3,97	3,87	3,79	3,73	3,68	3,63	3,60	3,57
	5,32	4,46	4,07	3,84	3,69	3,58	3,50	3,44	3,39	3,34	3,31	3,28
	5,12	4,26	3,86	3,63	3,48	3,37	3,29	3,23	3,18	3,13	3,10	3,07
	4,96	4,10	3,71	3,48	3,33	3,22	3,14	3,07	3,02	2,97	2,94	2,91
	4,84	3,98	3,59	3,36	3,20	3,09	3,01	2,95	2,90	2,86	2,82	2,79
	4,75	3,88	3,49	3,26	3,11	3,00	2,92	2,85	2,80	2,76	2,72	2,69
	4,67	3,80	3,41	3,18	3,02	2,92	2,84	2,77	2,72	2,67	2,63	2,60
	4,60	3,74	3,34	3,11	2,96	2,85	2,77	2,70	2,65	2,60	2,56	2,53
	4,54	3,68	3,29	3,06	2,90	2,79	2,70	2,64	2,59	2,55	2,51	2,48
	4,49	3,63	3,24	3,01	2,85	2,74	2,66	2,59	2,54	2,49	2,45	2,42
	4,45	3,59	3,20	2,96	2,81	2,70	2,62	2,55	2,50	2,45	2,41	2,38

СОДЕРЖАНИЕ

1. Элементы комбинаторики…………………………………………………
1.1. Размещения…………………………………………………………………
1.2 Понятие факториала………………………………………………………..
1.3 Размещения с повторениями………………………………………………
1.4 Сочетания…………………………………………………………………...
1.5 Сочетания с повторениями………………………………………………...
1.6 Перестановки……………………………………………………………….
1.7 Перестановки с повторениями………………………………………….…
Задачи к теме 1………………………………………………………………….

2. Элементы теории вероятностей………………………………………….
2.1. Классификация событий. Классическое определение вероятности. Свойства вероятности………………………………………………………….
2.2. Правила сложения и умножения вероятностей. Зависимые и независимые события…………………………………………………….…….
Задачи к теме 2………………………………………………………………….

3. Формулы полной вероятности и Байеса…………………………………
Задачи к теме 3………………………………………………………………….

4. Дискретные случайные величины……………………………………….
4.1. Определение дискретной случайной величины………………………….
4.2. Числовые характеристики………………………………..……………….
4.3. Математические операции над случайными величинами………………
4.4. Распределение Бернулли и Пуассона………………………………….….
4.5. Гипергеометрическое распределение…………………………………….
Задачи к теме 4……………………………………………………………….…

5. Непрерывные случайные величины………………………………….…
5.1. Функции распределения и плотность распределения непрерывной случайной величины……………………………………………………………
5.2. Нормальное распределение………………………………………………..
Задачи к теме 5………………………………………………………………….

6. Вариационные ряды и их характеристики……………………………...
6.1. Понятие вариационного ряда. Виды вариационных рядов………….….
6.2. Числовые характеристики вариационного ряда………………………….
Задачи к теме 6………………………………………………………………….
7. Выборочный метод и статистическое оценивание……………………..
7.1. Основные понятия и определения выборочного метода………………...
7.2. Статистическое оценивание……………………………………………….
7.3. Ошибки выборки…………………………………………………………...
7.4. Определение численности (объема) выборки……………………………
7.5. Интервальное оценивание…………………………………………………
Задачи к теме 7………………………………………………………………….

8. Проверка статистических гипотез………………………………………..
Задачи к теме 8………………………………………………………………….

Литература……………………………………………………………………...

Приложения…………………………………………………………………….	113
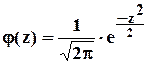Приложение 1. Таблица значений функции …………. Приложение 2. Таблица значений функции 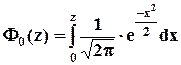(функция Лапласа)………………………………….. Приложение 3. Таблица значений функции Пуассона: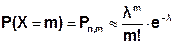………………………………………...……. Приложение 4. Критические точки распределения c²…………………… Приложение 5. Критические точки распределения Стьюдента………... Приложение 6. Критические точки распределения Фишера-Снедекора………………………………………………………………….……

Задание для самостоятельной работы по теории вероятностей и математической статистике

Лицензия ЛР № 020276 от 18.02.97 Государственного комитета Российской Федерации по печати

344000, г. Ростов – на - Дону, ул. Б. Садовая,69. РГЭУ. РИО

Отпечатано в КМЦ “Колибри”. 344000, г. Ростов – на – Дону, ул. Б. Садовая,79

[1] Выводы формул для числа размещений, а в последующем изложении - для числа сочетаний, - опускаются. Их можно найти в курсе элементарной алгебры.

[2] В учебниках по математической статистике вместо термина “статистическая совокупность” используется термин “набор данных”, а вместо термина “единица совокупности” используется термин “элемент выборки”.

[3] Для того, чтобы любые статистики служили хорошими оценками параметров генеральной совокупности, они должны обладать рядом свойств: несмещённости, эффективности, состоятельности, достаточности. Всем указанным свойствам отвечает выборочная средняя. s²_выб. -смещённая оценка. Для устранения смещения при малых выборках вводится поправка n¤ n-1 (cм. 7.1.).

[4] В литературе (1 - n /N) иногда называется "поправкой на бесповторность отбора".

[5] Для нормально распределенной случайной величины а. Поэтому справедливо:.

[6] В этой работе рассматриваются первые два типа гипотез.

[7] Эти гипотезы часто называют параметрическими, тогда как все остальные - непараметрическими.