
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Канонические формы представления логических функций
|
|
|
|
ВВЕДЕНИЕ
Разработка любого радиоэлектронного устройства сопровождается физическим или математическим моделированием. Физическое моделирование связано с большими материальными затратами, поскольку требуется изготовление макетов и их трудоемкое исследование. Часто физическое моделирование просто невозможно из-за чрезвычайной сложности устройства, например, при разработке больших и сверхбольших интегральных микросхем. В этом случае прибегают к математическому моделированию с использованием средств и методов вычислительной техники. Например, известный пакет P-CAD содержит блок логического моделирования цифровых устройств, однако для начинающих, в том числе и для студентов, он представляет значительные трудности в освоении. Не меньшие трудности встречаются и при использовании системы DesignLab.
Поскольку данное учебное пособие предназначено для студентов младших курсов, еще не получивших углубленные знания в специальных дисциплинах, в качестве основного инструментария для выполнения лабораторных и курсовых работ авторами пособия рекомендуется программа Electro-nics Workbench (EWB) как отличающаяся самым простым и легко осваиваемым пользовательским интерфейсом.
Electronics Workbench (EWB) — разработка фирмы Interactive Image Technologies (www.interactiv.com). Особенностью программы является наличие контрольно-измерительных приборов, по внешнему виду и характеристикам приближенных к их промышленным аналогам. Программа легко осваивается и достаточно удобна в работе. После составления схемы и ее упрощения путем оформления подсхем моделирование начинается щелчком обычного выключателя.
Для выполнения заданий контрольной работы студенту необходимо либо взять установочные файлы EWB у администратора локальной сети 3 корпуса либо скачать версию 5.12 с официального сайта.
Собранные схемы в формате EWB необходимо предъявить преподавателю после проверки контрольной работы во время зачета.
1. СИНТЕЗ КОМБИНАЦИОННЫХ УСТРОЙСТВ
Синтез логического устройства распадается на несколько этапов.
На первом этапе функцию, заданную в словесной, табличной или других формах, требуется представить в виде логического выражения с использованием некоторого базиса.
Дальнейшие этапы сводятся к получению минимальных форм функций, обеспечивающих при синтезе наименьшее количество электронного оборудования и рациональное построение функциональной схемы устройства. Для первого этапа обычно используется базис И, ИЛИ, НЕ независимо от базиса, который будет использован для построения логического устройства.
Для удобства последующих преобразований приняты следующие две исходные канонические формы представления функций: совершенная дизъюнктивная нормальная форма (СДНФ) и совершенная конъюнктивная нормальная форма (СКНФ).
Совершенная дизъюнктивная нормальная форма (СДНФ). Дизъюнктивной нормальной формой (ДНФ) называется такая форма представления функции, при которой логическое выражение функции строится в виде дизъюнкции ряда членов, каждый из которых является простой конъюнкцией аргументов или их инверсий.
Если исходная функция задана в табличной форме, то СДНФ может быть получена непосредственно.
Таблица 1

Пусть задана функция в форме табл. 1. Для этой функции СДНФ имеет вид
 (1)
(1)
Каждый член в выражении (1) соответствует некоторому набору значений аргументов, при котором 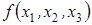 равна 1. Каждый из наборов аргументов, при которых
равна 1. Каждый из наборов аргументов, при которых 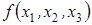 равна 1 (3-й, 4-й, 6-й, 8-й столбцы наборов), обращает в единицу соответствующий член выражения (1), вследствие чего и вся функция оказывается равной единице.
равна 1 (3-й, 4-й, 6-й, 8-й столбцы наборов), обращает в единицу соответствующий член выражения (1), вследствие чего и вся функция оказывается равной единице.
Можно сформулировать следующее правило записи СДНФ функции, заданной таблицей истинности. Необходимо записать столько членов в виде конъюнкций всех аргументов, сколько единиц содержит функция в таблице. Каждая конъюнкция должна соответствовать определенному набору значений аргументов, обращающему функцию в единицу, и если в этом наборе значение аргумента равно нулю, то в конъюнкцию входит инверсия данного аргумента.
Следует отметить, что любая функция имеет единственную СДНФ.
Совершенная конъюнктивная нормальная форма (СКНФ). Конъюнктивной нормальной формой (КНФ) называется форма представления функции в виде конъюнкции ряда членов, каждый из которых является простой дизъюнкцией аргументов (или их инверсий).
Рассмотрим в качестве примера функцию, приведенную в табл. 1.
 (2)
(2)
Выражение (2) содержит столько членов, связанных операцией конъюнкции, сколько нулей имеется среди значений функции 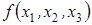 в таблице истинности. Каждому набору значении аргументов, на котором функция равна нулю, соответствует определенный член СКНФ, принимающий на этом наборе значений нуль. Так как члены СКНФ связаны операцией конъюнкции, то при обращении в нуль одного из членов функция оказывается равной нулю.
в таблице истинности. Каждому набору значении аргументов, на котором функция равна нулю, соответствует определенный член СКНФ, принимающий на этом наборе значений нуль. Так как члены СКНФ связаны операцией конъюнкции, то при обращении в нуль одного из членов функция оказывается равной нулю.
Таким образом, можно сформулировать правило записи СКНФ функции, заданной таблицей истинности. Следует записать столько конъюнктивных членов, представляющих собой дизъюнкции всех аргументов, при скольких наборах значений аргументов функция равна нулю, и если в наборе значение аргумента равно единице, то в дизъюнкцию входит инверсия этого аргумента. Любая функция имеет единственную СКНФ.
Структурная схема логического устройства может быть построена непосредственно по канонической форме (СДНФ или СКНФ) реализуемой функции. Получающиеся при этом схемы для функций (1) и (2) показаны на рис. 1а, б. Недостаток такого метода построения структурных схем, обеспечивающего в общем правильное функционирование устройства, состоит в том, что получающиеся схемы чаще всего неоправданно сложные, требуют использования большого числа логических элементов, имеют низкие экономичность и надежность. Во многих случаях удается так упростить логическое выражение, не изменив функции, что соответствующая структурная схема оказывается существенно более простой. Методы такого упрощения функции называются методами минимизации функций.
|
|
|
|
|
Дата добавления: 2014-10-22; Просмотров: 1783; Нарушение авторских прав?; Мы поможем в написании вашей работы!