Минимизация функций с использованием карт Карно

Отличие карт Карно от карт Вейча заключается в способе обозначе­ния строк и столбцов таблицы истинности. Таблица 15 иллюстрирует карты Карно для функций трех и четырех аргументов.

Аргументы функции делятся на две группы, комбинации значений аргументов одной группы приписываются столбцам таблицы, комбина­ции значений аргументов другой группы - строкам таблицы. Столбцы и строки обозначаются комбинациями, соответствующими последова­тельности чисел в коде Грея (это сделано для того, чтобы склеивающиеся клетки находились рядом). Обозначения столбца и строки, на пересече­нии которых находится клетка таблицы, образуют набор, значение функции на этом наборе записывается в клетку.

Для получения МДНФ функции охватываются областями клетки таблицы, содержащие 1. Как и в случае минимизации с помощью карт Вейча, области должны быть прямоугольной формы и содержать 2^k клеток (при целочисленном значении k). Для каждой области составля­ется набор из двух комбинаций: приписанных столбцам и приписанных строкам, на пересечении которых расположена область. При этом если области соответствуют несколько комбинаций кода Грея, приписанных столбцам или строкам, то при составлении набора области записывает­ся общая часть этих комбинаций, а на месте различающихся разрядов комбинаций ставятся звездочки. Например, для функции, представлен­ной табл. 16, области I будет соответствовать набор 1*00 или член МДНФ 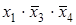, области II - набор 0**1 или член МДНФ 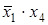. Таким образом, для этой функции МДНФ

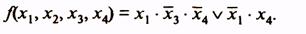
Таблица 15

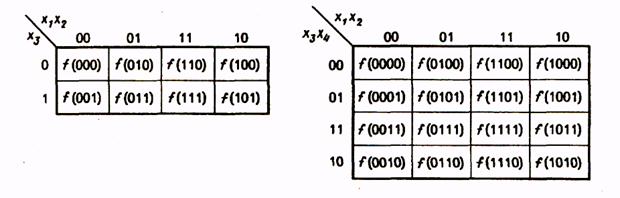
Таблица 16Таблица 17

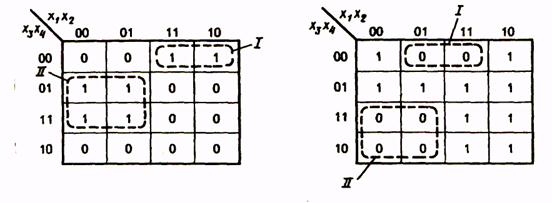
Для получения МКНФ областями охватываются клетки, содержа­щие 0, и члены МКНФ записываются через инверсии цифр, получаемых для наборов отдельных областей. Так, для функции, представленной в табл. 17, области I соответствует набор *100 и член МКНФ 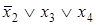, области II — набор О*1* и член 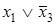. Таким образом, МКНФ функции

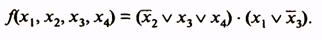
1.5. Задание для выполнения

Для функции четырех аргументов F(x1,x2,x2,x4):

а) записать СДНФ;

б) записать СКНФ;

в) упростить функцию с помощью метода Квайна – записать МДНФ и МКНФ;

г) упростить функцию с помощью карты Вейча – записать МДНФ и МКНФ;

д) упростить функцию с помощью карты Карно – записать МДНФ и МКНФ;

е) сравнить МДНФ и МКНФ, полученные в п. в)-д);

ж) реализовать МДНФ и МКНФ на логических элементах.

Для выбора варианта взять 2 последние цифры в номере зачетной книжки.

x1	№ варианта
x2
x3
x4
F(x1,x2,x3,x4)	1,21,41,61
F(x1,x2,x3,x4)	2,22,42,62
F(x1,x2,x3,x4)	3,23,43,63
F(x1,x2,x3,x4)	4,24,44,64
F(x1,x2,x3,x4)	5,25,45,65
F(x1,x2,x3,x4)	6,26,46,66
F(x1,x2,x3,x4)	7,27,47,67
F(x1,x2,x3,x4)	8,28,48,68
F(x1,x2,x3,x4)	9,29,49,69
F(x1,x2,x3,x4)	10,30,50,70
F(x1,x2,x3,x4)	11,31,51,71
F(x1,x2,x3,x4)	12,32,52,72
F(x1,x2,x3,x4)	13,33,53,73
F(x1,x2,x3,x4)	14,34,54,74
F(x1,x2,x3,x4)	15,35,55,75
F(x1,x2,x3,x4)	16,36,56,76
F(x1,x2,x3,x4)	17,37,57,77
F(x1,x2,x3,x4)	18,38,58,78
F(x1,x2,x3,x4)	19,39,59,79
F(x1,x2,x3,x4)	20,40,60,80

Дата добавления: 2014-10-22