Минимизация логических функций методом карт Вейча

Метод минимизации функции с помощью карт Вейча обеспечивает простоту получения результатов. Он используется при минимизации относительно несложных функций (с числом аргументов до пяти). Карта Вейча представляет собой опре­деленную форму таблицы истинности. Табл. 6 являются картами Вейча для функций соответственно двух (а), трех (б), четырех (в) аргу­ментов.

Таблица 6

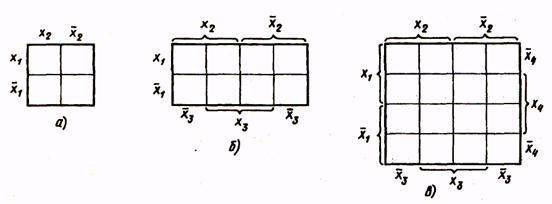
Каждая клетка карты соответствует некоторому набору значений аргументов. Этот набор аргументов определяется присвоением значе­ния лог.1 буквам, на пересечении строк и столбцов которых расположе­на клетка. Так, в карте функций четырех аргументов (табл. 6в) клетки первой строки соответствуют следующим комбинациям значе­ний аргументов:

1-я клетка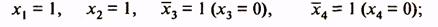

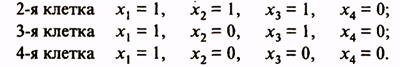
Число клеток карты равно числу всех возможных наборов значений аргументов 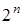(п — число аргументов функций). В каждую из клеток карты записывается значение функции на соответствующем этой клетке наборе значений аргументов. Пусть функция задана таблицей истиннос­ти (табл. 7). Таблица истин­ности этой функции в форме карты Вейча представлена табл. 8.

Таблица 7

Карта Вейча определяет значения функции на всех возмож­ных наборах значений аргументов и является таблицей истинности. Карты Вейча компактны, но главное их достоинство состоит в следующем. При любом переходе из одной клетки в соседнюю вдоль столбца или строки изменяется значение лишь одного аргумента функции. Следовательно, если в паре соседних клеток содержится 1, то над соответствующими им членами канонической формы может быть проведена операция склеива­ния. Таким образом, облегчается поиск склеиваемых членов.

Таблица 8Таблица 9

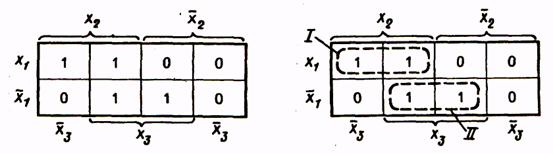
Сформулируем правила получения МДНФ функций с помощью карт Вейча. Все клетки, содержащие 1, объединяются в замкнутые области. При этом каждая область должна представлять собой прямоугольник с чис­лом клеток 2 ^k, где k - 0, 1, 2,.... Значит, допустимое число клеток в области 1, 2, 4, 8,...,. Области могут пересекаться и одни и те же клетки могут входить в разные области. Затем проводится запись выражения МДНФ функции. Каждая из областей в МДНФ представляется членом, число букв в котором на k меньше общего числа аргументов функции п (т.е. равно 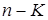). Каждый член МДНФ составляется лишь из тех аргу­ментов, которые для клеток соответствующей области имеют одинако­вое значение (без инверсии либо с инверсией).

Таким образом, при охвате клеток замкнутыми областями следует стремиться, чтобы число областей было минимальным (при этом мини­мальным будет число членов в МДНФ функции), а каждая область содержала возможно большее число клеток (при этом минимальным будет число букв в членах МДНФ функции).

Рассмотрим минимизацию с помощью карты Вейча функции трех аргументов, представленной табл. 9. Все клетки, содержащие 1, охва­тываются двумя областями. В каждой из областей 2¹ клеток, для них n-k = 3-l = 2, и эти области в МДНФ будут представлены членами, содержащими по две буквы. Первой области соответствует член 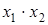(аргумент 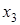здесь не присутствует, так как для одной клетки этой области он имеет значение без инверсии, для другой — с инверсией); второй области соответствует член 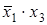. Следовательно, МДНФ функ­ции

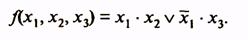
Рассмотрим пример минимизации функции четырех аргументов, заданной табл. 10. Первая и четвертая области имеют по две клетки, для них п- k - 4 -1=3. Эти области в МДНФ будут представлены членами, содержащими по три буквы. Вторая и третья области содер­жат по четыре клетки и в МДНФ выражаются членами, содержащими по две буквы (п - k = 4 -2 = 2). Минимальная ДНФ функции

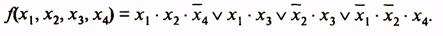
Таблица 10Таблица 11

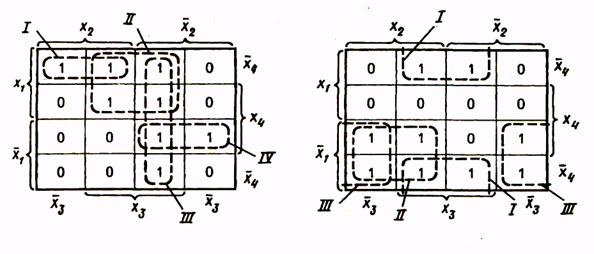
При построении замкнутых областей допускается сворачивание карты в цилиндр с объединением ее противоположных граней. В силу этого крайние клетки строки или столбца таблицы рассматриваются как соседние и могут быть объединены в общую область. Иллюстрацию этого приема проведем на примере функции, представленной табл. 11. Минимальная ДНФ функции

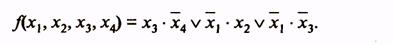
В силу допустимости такого сворачивания карты вдоль горизонталь­ной и вертикальной осей, например: клетки, расположенные в четырех углах карты функции четырех переменных, оказываются соседними и могут быть объединены в одну область. Покажем это на примере мини­мизации функции, заданной табл. 12. Минимальная ДНФ функции

Таблица 12Таблица 13

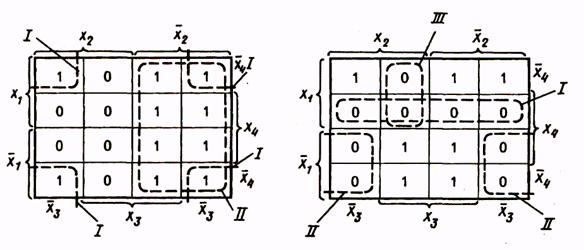
Для получения МКНФ функции замкнутыми областями охватыва­ются клетки с нулевыми значениями функции, и при записи членов логического выражения берутся инверсии аргументов, на пересечении которых находятся области. Так, для функции, приведенной в табл. 13, МКНФ

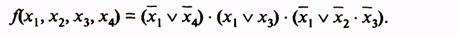
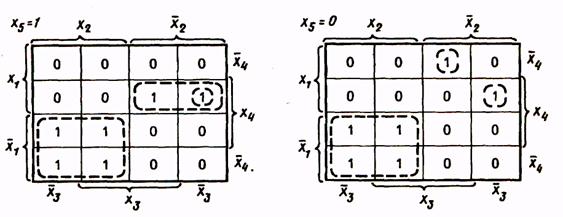
До сих пор рассматривались логические функции с числом аргумен­тов до четырех. Представление функции и минимизация ее с помощью карт Вейча усложняются, если число аргументов больше четырех. В табл. 14 показано представление с помощью карт Вейча функции пяти аргументов.

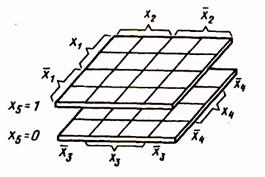Рис.3

Таблица истинности здесь состоит из двух карт, каж­дая из которых представляет собой карту четырех переменных. Одна из них соответствует х5= 1, другая - х5 = 0. Эти карты можно мысленно расположить одна над другой (рис.3). При этом области охвата клеток могут быть трехмерными, т.е. одной областью могут охваты­ваться клетки двух карт.

Для функции, приведенной в табл. 23, МДНФ

Таблица 14

Для минимизации функции с числом аргументов, большим пяти, карты Вейча оказываются неудобными. Минимизация таких функций может быть выполнена методом Квайна.

Дата добавления: 2014-10-22