Минимизация логических функций методом Квайна

Метод Квайна позволяет представлять функции в ДНФ или КНФ с минимальным числом членов и минимальным числом букв в членах.

Этот метод содержит два этапа преобразования выражения функции: на первом этапе осуществляется переход от канонической формы (СДНФ или СКНФ) к так называемой сокращенной форме, на втором этапе - переход от сокращенной формы логического выражения к минимальной форме.

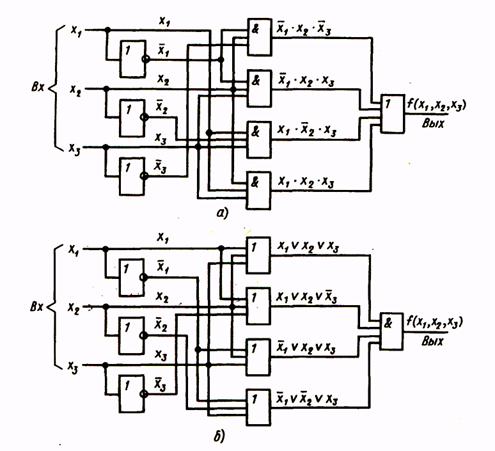
Рис. 1

Первый этап (получение сокращенной формы). Пусть заданная функ­ция представлена в СДНФ. Переход к сокращенной форме основан на последовательном применении двух операций: операции склеивания и операции поглощения.

Для выполнения операции склеивания в выражении функции выяв­ляются пары членов вида 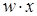и 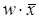, различающихся лишь тем, что один из аргументов в одном из членов представлен без инверсии, а в другом - с инверсией. Затем проводится склеивание таких пар чле­нов: 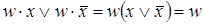, и результаты склеивания w вводятся в выражение функции в качестве дополнительных членов. Далее выполняется операция поглощения. Она основана на равенстве 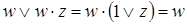(член w поглощает член 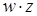). При проведении этой операции из логического выражения вычеркиваются все члены, поглощаемые членами, которые введены в результате операции скле­ивания.

Операции склеивания и поглощения выполняются последовательно до тех пор, пока это возможно. Покажем этот этап минимизации логичес­кого выражения на примере построения логического устройства для функции, заданной в табл. 2.

Таблица 2

Совершенная ДНФ этой функции

(3)

Для получения сокращенной формы проводим операции склеивания и поглощения:

(4)

Второй этап (получение минимальной формы). Выражение (4) представляет собой сокращенную форму логичес­кого выражения заданной функции, а члены его являются простыми импликантами функции. Переход от сокращенной формы к минималь­ной осуществляется с помощью импликантной матрицы, приведенной в табл. 3.

Таблица 3

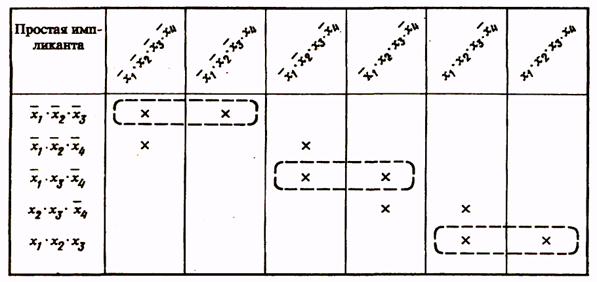
В столбцы импликантной матрицы вписываются члены СДНФ за­данной функции, в строки - простые импликанты функции, т.е. члены сокращенной формы логического выражения функции. Отмечаются (например, крестиками) столбцы членов СДНФ, поглощаемых отдельными простыми импликантами. В табл. 3 простая импликанта 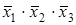поглощает члены 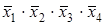, 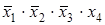(в первом и во втором столбцах первой строки поставлены крестики).

Вторая импликанта поглощает 1-й и 3-й члены СДНФ (крес­тики поставлены в первом и третьем столбцах второй строки) и т.д. Импликанты, которые не могут быть лишними и, следовательно, не могут быть исключены из сокращенной формы, составляют ядро. Вхо­дящие в ядро импликанты легко определяются по импликантной матри­це. Для каждой из них имеется хотя бы один столбец, перекрываемый только данной импликантой.

В рассматриваемом примере ядро составляют импликанты 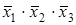и 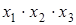(только ими перекрываются второй и шестой столбцы матрицы). Исключение из сокращенной формы одновременно всех импликант, не входящих в ядро, невозможно, так как исключение одной из импликант может превратить другую уже в нелишний член.

Для получения минимальной формы достаточно выбрать из импли­кант, не входящих в ядро, такое минимальное их число с минимальным количеством букв в каждой из этих импликант, которое обеспечит пере­крытие всех столбцов, не перекрытых членами ядра. В рассматриваемом примере необходимо импликантами, не входящими в ядро, перекрыть третий и четвертый столбцы матрицы. Это может быть достигнуто различными способами, но, так как необходимо выбирать минимальное число импликант, то, очевидно, для перекрытия этих столбцов следует выбрать импликанту .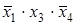

Минимальная дизъюнктивная нормальная форма (МДНФ) заданной функции

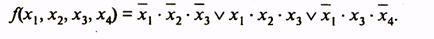(5)

Структурная схема, соответствующая этому выражению, приведена на рис.2.

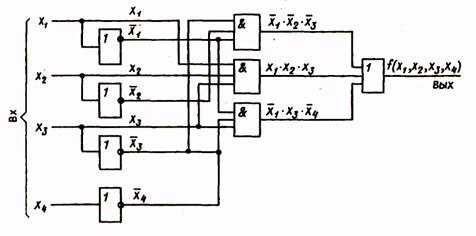
Рис. 2

До сих пор рассматривалось получение минимальной ДНФ. При использовании метода Квайна для получения минимальной конъюнктивной нормальной формы (МКНФ) логической функции имеются следую­щие особенности:

- исходной для минимизации формой логического выражения задан­ной функции является СКНФ;

- пары склеиваемых членов имеют вид w v д: и wv x;

- операция поглощения проводится в соответствии с выражением

Рассмотрим применение метода Квайна на примере минимизации функции, заданной таблицей истинности (табл. 4).

Таблица 4

Совершенная КНФ рассматриваемой функции

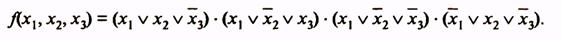
Склеивающиеся пары членов:

1-й и 3-й члены (результат склеивания );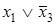

1-й и 4-й члены (результат склеивания );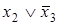

2-й и 3-й члены (результат склеивания ).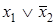

Проводим операции склеивания и поглощения:

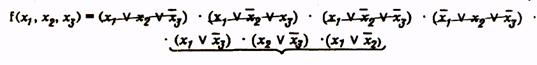
Члены операции склеивания

Полученное выражение является сокращенной формой функции.

Для перехода к минимальной форме строим импликантную матрицу (табл. 5).

Таблица 5

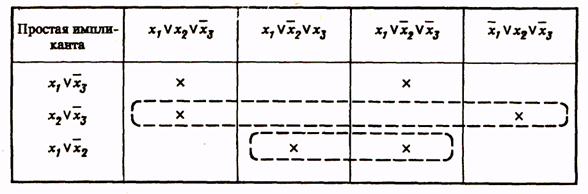
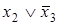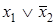Все столбцы матрицы перекрываются импликантами и . Следовательно, член 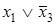является лишним и минимальная конъюнктивная нормальная форма (МКНФ) заданной функции

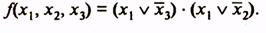
Дата добавления: 2014-10-22