Основные определения и формулы

ФОРМУЛА БАЙЕСА

Лабораторная работа

Случайным событием называется такое событие, которое может произойти или не произойти в результате некоторого опыта.

Случайные события называют несовместными в данном испытании, если появление одного из них исключает появление других событий в одном и том же испытании.

Случайные события образуют полную группу, если при каждом испытании может появиться любое из них и не может появиться какое-либо иное событие несовместное с ними.

Вероятностью Р события А называется отношение числа m благоприятствующих случаев к числу всех возможных случаев

(1)

Сумма вероятностей случайных событий B₁, B₂,…B_n,

образующих полную группу, равна единице

Событие А называется зависимым от события В, если вероятность появления события А зависит от того, произошло или не произошло событие В.

Вероятность того, что произошло событие А при условии,что произошло событие В, будем обозначать P(A/B) и называть условной вероятностью события А при условии В.

Рассмотрим полную группу несовместных событий В₁, В₂, …, В_n, вероятности появления которых P(B₁), P(B₂), …, P(B_n). Поскольку заранее неизвестно, какое из этих событий наступит, их называют гипотезами. Событие А может наступить в каком-либо опыте вместе с одной из гипотез событий В₁, В₂, …, В_n. Вероятность события А вычисляется по формуле полной вероятности

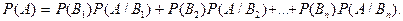(2)

После опыта (апостериорно) стало известно, что событие А появилось, следует выяснить, вместе с какой из гипотез B₁,…, B_n оно произошло. По постановке задача напоминает диагностику причины по известному следствию.

P(Bi), i=1,…n - априорные (доопытные) вероятности гипотез

P(Bi / A), i=1,…n - апостериорные вероятности гипотез (сформировавшиеся после опыта)

Найдем апостериорные вероятности гипотез P(Bi / A), i=1,…n.

По формуле умножения вероятностей найдем вероятность совмещения событий B и А

P(B_i A)=P(B_i) P(A / B_i)=P(A) P(B_i/A).

Из последнего равенства выразим апостериорную вероятность гипотезы В

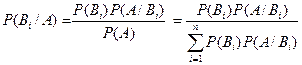(3)

Получили формулы Байеса. Формулы Байеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, т.е. провести коррекцию вероятностей априорных гипотез, используя экспериментальные данные.

I. Задача.

Имеются три одинаковые на вид урны. В первой урне – 2 белых и 1 черный шар, во второй – 3 белых и 1 черный, в третьей – 2 белых и 2 черных. Некто наудачу вынимает шар из урны. Найти вероятность того, что шар белый.

Решение. Событие А – извлечение белогошара.

Выдвинем гипотезы:

B₁ – шар выбран из первой урны;

B₂ – шар выбран из второй урны;

B₃ – шар выбран из третьй урны.

Гипотезы равновероятны, т.е. во всех случаях m=1, n=3.

P(B₁)=P(B₂)=P(B₃)=1/3.

Вероятность извлечения белого шара из первой урны –условную вероятность - найдем по формуле классического определения вероятности (формула (1)), если m=2, n=3, P(А/B₁)=2/3;

из второй урны - m=3, n=4, P(А/B₂)=3/4;

из третьей урны - m=2, n=4, P(А/B₃)=2/4;

По формуле полной вероятности (2) находим вероятность появления события А

Р(А)=1/3*2/3+1/3*3/4+1/3*1/2.

Пусть теперь событие А произошло - из урны извлечен белый шар.

Найдем вероятность того, что этот шар извлечен из первой урны Р(В₁/А) по формуле (3).

Р(В₁/А)=(1/3*2/3)/Р(А).

Вычисления выполним на компьютере в программе EXCEL.

Для запуска программы EXCEL щелкнуть на кнопке Пуск-Программы –Microsoft Excel.

Дата добавления: 2014-10-22