Устойчивость систем управления

Дифференциальный закон управления

В этом случае 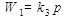или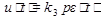

Передаточная функция может иметь более сложный вид

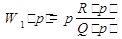
И в статическом режиме:

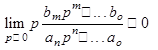
Передаточная функция разомкнутой системы

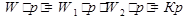
Выражение для ошибки

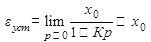
Таким образом, дифференциальное управление в чистом виде не применяется.

В общем случае может использоваться пропорционально-интегрально-дифференциальный (ПИД) закон управления:

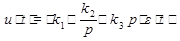
Понятие устойчивости

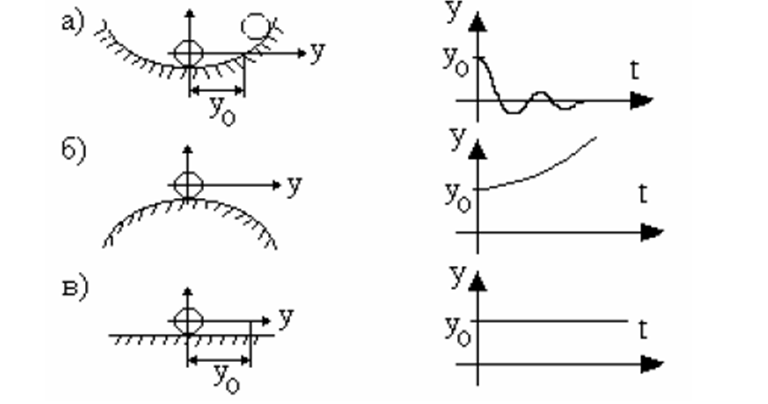
а) y(t)→0 при t→∞, устойчивое положение шарика;

б) y(t)→∞ при t→∞, неустойчивое положение шарика;

в) y(t)=y0=const при t≥0, нейтральное или безразличное положение шарика.

Определение устойчивости по корням характеристического уравнения

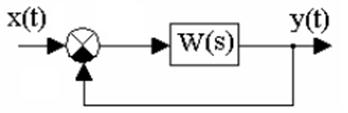
Выходной сигнал системы состоит из двух составляющих: y(t) = y_B(t) + y_п(t)

где y_B(t) – вынужденная составляющая (определяется входом x(t));

y_п(t) – переходная составляющая (определяется собственной динамикой системы).

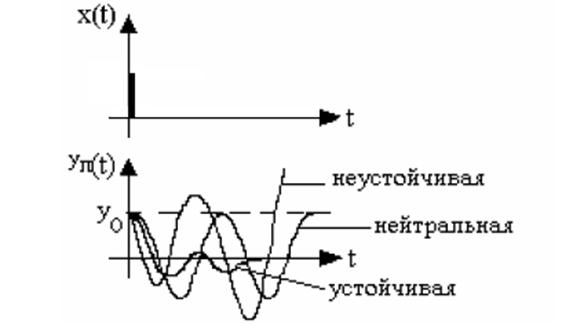
Переходная составляющая решения уравнения зависит от корней p_i характеристического уравнения: 1+W(p) = 0

В общем виде:

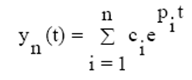
Возможны 3 случая:

1. Действительные корни характеристического уравнения

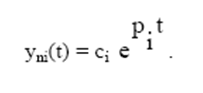
где p_i - корни характеристического уравнения (полюсы системы);

c_i - постоянные интегрирования.

если p_i > 0, то y_пi(t) ® ¥ при t ® ¥

если p_i < 0, то y_пi(t) ® 0 при t ® ¥

2. Пара комплексно-сопряженных корней

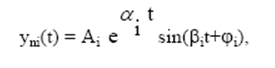
где α_i±jβ_i - корни характеристического уравнения;

A_i, j_i - постоянные интегрирования.

если α_i > 0, то y_пi(t) ® ¥ при t ® ¥

если α_i < 0, то y_пi(t) ® 0 при t ® ¥

3. Чисто мнимые корни

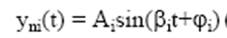
где β_i – мнимые корни характеристического уравнения;

A_i, j_i - постоянные интегрирования.

Переходная составляющая y_пi(t) имеет вид колебаний с постоянной амплитудой.

Таким образом, для устойчивости системы необходимо и достаточно, чтобы все корни характеристического уравнения имели отрицательные вещественные части, или эти корни на плоскости комплексного переменного были расположены слева от мнимой оси.

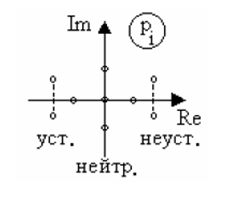
Условие устойчивости Стодолы: необходимым (но не достаточным) условием устойчивости системы является положительность (отрицательность) всех коэффициентов характеристического уравнения.

Границы устойчивости:

· нулевой корень p_i = 0 1-го типа;

· два мнимых корня p_i = jb 2-го типа;

· бесконечный корень p_i = ¥ 3-го типа.

Дата добавления: 2014-10-22