
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Понятие о дифференциальном уравнении
|
|
|
|
Вычисление объема тела вращения
Вычисление объема тела по известным площадям поперечных сечений.
Если площадь сечения тела плоскостьб, перпендикулярной оси Ох, выражена как функция от х, т.е. в виде S = S(х) (а<x<b), то объем части тела, заключенной между перпендикулярными оси Ох плоскостями х = а и х = b находят по формуле
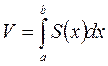
Если криволинейная трапеция, ограниченная кривой у = f(x) и прямыми х = а, х = b, у = 0, вращается вокруг оси Ох, то объем тела вращения вычисляется по формуле
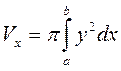
Если фигура, ограниченная кривыми у1 = f1(x) и у2 = f2(x) [0≤f1≤f2] и прямыми х = а, х = b, вращается вокруг оси Ох, то объем тела вращения вычисляется по формуле
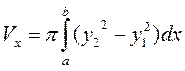
Определение. Уравнение, содержащее независимую переменную, функцию от этой независимой переменной и ее производные различных порядков, называется дифференциальным уравнением.
Определение. Наивысший порядок производной, входящей в дифференциальное уравнение, называется порядком дифференциального уравнения.
Дифференциальные уравнения широко применяются в области медицины: это волновые и колебательные движения, вязкость крови и т.д.
Определение. Решением дифференциального уравнения называется любая функция y = j(x), при подстановке которой в уравнение будет получено тождество. Процесс нахождения решения дифференциального уравнения называется интегрированием дифференциального уравнения, график решения называют интегральной кривой.
Интегральная кривая – это график решения дифференциального уравнения, т.е график функции, удовлетворяющей этому уравнению.
Общим решением дифференциального уравнения y∕ = j(x,у), в области определения D(f) называется функция y = j (x, С), обладающая следующими свойствами:
1. Она является решением данного уравнения при любых значениях произвольной постоянной С, принадлежащих некоторому множеству.
2. для любого начального условия у(х0) = х0: (х0, у0) Є D (f) 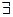 ! C = C0, при котором решение y = j (x, С0), удовлетворяет заданному условию.
! C = C0, при котором решение y = j (x, С0), удовлетворяет заданному условию.
Всякое решение y = j (x, С0), получается из общего решения y = j (x, С) при конкретном значении С = С0, называется частным решением дифференциального уравнения.
Пример 1: Найти частное решение дифференциального уравнения у/ = 2у – 6, если х = 0, у = 4.
Решение:
dу = 2(у-3) dх
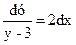
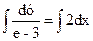 общее решение
общее решение
ln(у – 3) = 2х + С
ln(4 – 3) = 0 + С
C = ln 1 = 0
ln(у – 3) = 2х
2х = 2хlnе = lne2x
у – 3 = lne2x
у = lne2x + 3 – частное решение.
Дифференциальные уравнения описывают многие примеры самых разных процессов природы. Например: поглощение света в растворе, фармакологическая кинетика.
Пример 1: Найдем закон Т(t) остывания кипящей воды до комнатной температуры (tкомн=200) и время достижения 400, если до 600 вода остывает за 20 мин. Известно, что мгновенная скорость остывания линейно зависит от разницы Т и tкомн.
Решение:
Составим дифференциальное уравнение:
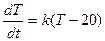
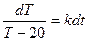
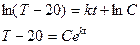
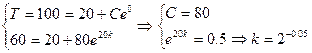
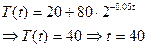
В медицинских приложениях дифференциальные уравнения используются для:
· определения скорости кровотока, скорости движения клапанов и стенок сердца (эхокардиография), определение вязкости крови и других параметров гемодинамики;
· описания медико- биологических приложений ультразвука: эхоэнцефалограмма, УЗИ, ультразвуковая физиотерапия, ультразвуковая локация и кардиография;
· описания процессов физиологической акустики, которая изучает устройство и работу звуковоспринимающих и звуковоспроизводящих органов человека и животных.
Составление дифференциальных уравнений на простых задачах
Решим уравнение 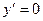 .
.
Его решение: 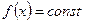 определено на
определено на 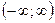 . Отметим, что эта постоянная – произвольная и решение – не единственное, а имеется бесконечное множество решений.
. Отметим, что эта постоянная – произвольная и решение – не единственное, а имеется бесконечное множество решений.
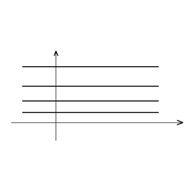 рис.1 рис.1
|
Более сложное уравнение, в котором производная непостоянная, имеет вид: 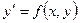 . Это – уравнение первого порядка, разрешенное относительно
. Это – уравнение первого порядка, разрешенное относительно 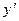 . (Термин «разрешенное» означает, что
. (Термин «разрешенное» означает, что 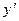 выражается через остальные величины, в отличие от уравнения общего вида
выражается через остальные величины, в отличие от уравнения общего вида 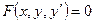 , из которого выразить
, из которого выразить 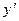 может быть и не удастся). Это уравнение также имеет бесконечно много решений, отличающихся на константу C (см. рис. 2):
может быть и не удастся). Это уравнение также имеет бесконечно много решений, отличающихся на константу C (см. рис. 2):
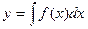
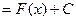 Это решение дифференциального уравнения описывается серией функций:
Это решение дифференциального уравнения описывается серией функций:
при С=0 y=F(x)
при С=1 y=F(x) + 1 и т.д. Таким образом серия графиков получена параллельным переносом на константу С.
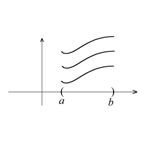 рис.2
рис.2
Более сложные дифференциальные уравнения обычно стараются свести к таким простейшим уравнениям 1-го порядка, разрешенным относительно производной, которые легко решить интегрированием.
|
|
|
|
|
Дата добавления: 2014-10-22; Просмотров: 689; Нарушение авторских прав?; Мы поможем в написании вашей работы!