Абсолютно и условно сходящиеся ряды

Важный класс сходящихся рядов образуют так называемые абсолютно сходящиеся ряды.

Определение: Ряд 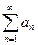называется абсолютно сходящимся, если сходится ряд 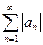. (Т.е. если ряд абсолютно сходится, то он и просто сходится).

Для исследования рядов на абсолютную сходимость можно использовать все признаки сходимости для рядов с неотрицательными членами.

Теорема1: Пусть для ряда 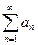выполняется условие .

Тогда, если q<1, то ряд сходится, а если q>1, то ряд расходится.

Теорема 2: если последовательность (а_n) из положительных чисел монотонно убывает и 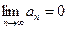, то ряд сходится.

Пример: Рассмотримряд , где α >1.

Этот ряд сходится и, более того, сходится абсолютно. Действительно, здесь и ряд 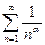, где α >1., сходится. Следовательно, данный ряд сходится абсолютно и, в частности, он сходится.

Ряд называется условно сходящимся, если он является сходящимся, но не является абсолютно сходящимся.

Например, оба ряда 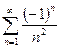и сходятся. Однако, если первый ряд абсолютно сходится, то второй ряд не является абсолютно сходящимся и, следовательно, является условно сходящимся.

Дата добавления: 2014-10-22