
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные статистические характеристики случайных процессов
|
|
|
|
Стационарные реализации случайного процесса
Эргодические случайные процессы
Только стационарные процессы обладают свойством эргодичности. Если случайный процесс стационарен, определен формулами (9.1) и (9.2) и при этом функции m и R одинаковы для различных выборочных функций, процесс является эргодическим.
При исследовании случайных процессов на практике говорят о стационарности или нестационарности процесса по одной реализации выборочной функции. Стационарность означает, что характеристики, рассчитанные по коротким отрезкам времени, не меняются значимо для других отрезков.

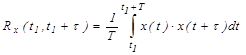
Для описания основных свойств СЛП используются 4 статистические функции:
1) среднее значение квадрата случайного процесса;
2) плотность распределения;
3) автокорреляционная функция;
4) спектральная плотность.
Третья и четвертая функции формально одно и то же. Они связаны через преобразование Фурье, однако дают информацию различного типа: третья функция – о процессе во временной области; четвертая – о процессе в частотной области.
Первая функция дает элементарное представление об интенсивности процесса, а вторая – характеризует распределение вероятности процесса в фиксированных точках.
1)  , где Т – интервал продолжительности.
, где Т – интервал продолжительности.
2) Плотность распределения определяет вероятность того, что значения процесса в произвольный момент времени будут заключены в определенном интервале:
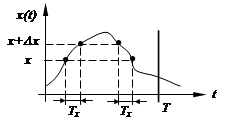
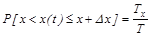 ,
,
где D х – интервал;
Т – время рассмотрения процесса;
Тх – суммарная продолжительность нахождения процесса в интервале D х.
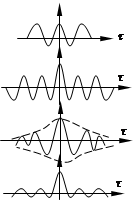 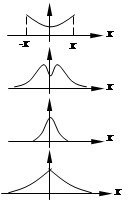 процесс процесс
| Р(х) | Rx(t) | Gx(f) |
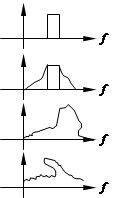 
|
|
|
|
|
|
Дата добавления: 2014-10-22; Просмотров: 347; Нарушение авторских прав?; Мы поможем в написании вашей работы!