
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные уравнения электростатического поля и его характеристики
|
|
|
|
В лекции изложены уравнения электростатического поля, закон Кулона, расчёт поля по заданному распределению зарядов. Получены уравнения Лапласа - Пуассона для описания и исследования потенциальных электростатических полей. Изложены граничные условия на границе раздела сред с различными физическими свойствами.
Электростатическое поле-это частный вид электромагнитного поля. Оно создается совокупностью электрических зарядов, неподвижных в пространстве по отношению к наблюдателю и неизменных во времени.
Электростатическое поле обладает способностью воздействовать на помещенные в него электрический заряд с механической силой, прямо пропорциональной значению этого заряда. В основу определения электростатического поля положено механическое его проявление. Оно описывается законом Кулона.
Закон Кулона. Два точечных заряда  и
и  в вакууме взаимодействуют друг с другом с силой
в вакууме взаимодействуют друг с другом с силой 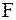 , прямо пропорциональной произведению зарядов
, прямо пропорциональной произведению зарядов  и
и  и обратно пропорциональной квадрату расстояния r между ними. Эта сила направлена по линии, соединяющей точечные заряды (рис.4).
и обратно пропорциональной квадрату расстояния r между ними. Эта сила направлена по линии, соединяющей точечные заряды (рис.4).

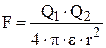 ,
,
где 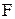 - кулоновская сила (Н);
- кулоновская сила (Н); 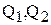 — заряды (Кл);
— заряды (Кл); 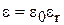 — диэлектрическая постоянная (Ф/м);
— диэлектрическая постоянная (Ф/м);  (Ф/м) — диэлектрическая постоянная вакуума;
(Ф/м) — диэлектрическая постоянная вакуума;  -относительная диэлектрическая проницаемость среды;
-относительная диэлектрическая проницаемость среды;  - расстояние между заряженными телами (м).
- расстояние между заряженными телами (м).
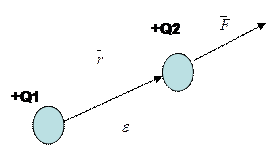
Рис. 4
В векторной форме закон Кулона имеет вид:

Где  - единичный вектор, направленный по линии, соединяющей заряды.
- единичный вектор, направленный по линии, соединяющей заряды.
Закон Кулона справедлив только для однородных и изотропных сред.
Основными величинами для электростатического поля является напряженность  и потенциал
и потенциал 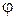 . Напряженность электростатического поля- величина векторная, определяемая в каждой точке значением и направлением; потенциал является величиной скалярной. Значение потенциала определяется в каждой точке поля некоторым числом.
. Напряженность электростатического поля- величина векторная, определяемая в каждой точке значением и направлением; потенциал является величиной скалярной. Значение потенциала определяется в каждой точке поля некоторым числом.
Напряженность  - это силовая характеристика электростатического поля. Она определяется следующим образом:
- это силовая характеристика электростатического поля. Она определяется следующим образом:
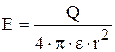
или в векторной форме
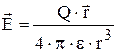 .
.
Расчет электростатического поля сводится к определению вектора напряженности поля 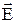 в каждой точке пространства, где существует поле.
в каждой точке пространства, где существует поле.
Энергетической характеристикой поля является – электрический потенциал 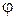 :
:
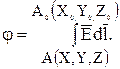
подставив в интеграл верхний предел, получим другое выражение для 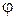 :
:
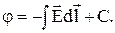
Выражение для потенциала свидетельствует о том, что если вектор 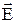 направлен в каждой точке по нормали к кривой
направлен в каждой точке по нормали к кривой 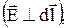 то для всей этой кривой (рис.5):
то для всей этой кривой (рис.5):
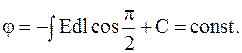
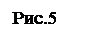

Кривую типа  называютлинией равного потенциала.
называютлинией равного потенциала.
Расчёт поля и потенциалов по заданному распределению зарядов приведен в табл. 2.
Таблица 2
| Распределение зарядов | Плотность заряда | Заряд | Напряжённость | Потенциал |
| В объёме V | Объемная  (К/м3) (К/м3)
| 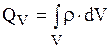
| 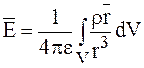
| 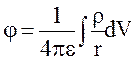
|
| На бесконечно тонких поверхностных слоях | Поверхностная  (К/м2) (К/м2)
| 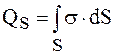
| 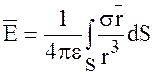
| 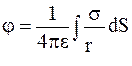 
|
| Вдоль линии | Линейная 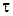 (К/м) (К/м)
| 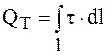
| 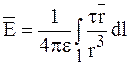
| 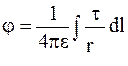
|
Между вектором напряжённости и потенциалом существует связь дифференциального вида: 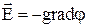 . Данное соотношение можно истолковать следующим образом: напряженность в какой- либо точке поля равна скорости изменения потенциала в этой точке поля, взятой с обратным знаком. Знак минус означает, что направление вектора
. Данное соотношение можно истолковать следующим образом: напряженность в какой- либо точке поля равна скорости изменения потенциала в этой точке поля, взятой с обратным знаком. Знак минус означает, что направление вектора 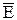 и направление
и направление  противоположны.
противоположны.
Одной из важнейших теорем электростатики является теорема Гаусса. Она соответствует закону Кулона и принципу наложения. Теорема формулируется так:
Поток вектора электрического смещения через любую замкнутую поверхность, окружающую некоторый объём, равен алгебраической сумме свободных зарядов, находящихся внутри этой поверхности.
В интегральной форме теорема имеет вид:
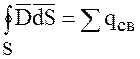
Где  -вектор электрической индукции.
-вектор электрической индукции.
Но с помощью этой формулы нельзя определить, как связан исток линий  в данной точке поля с плотностью свободных зарядов в той же точке поля. Ответ на этот вопрос даёт дифференциальная форма теоремы Гаусса:
в данной точке поля с плотностью свободных зарядов в той же точке поля. Ответ на этот вопрос даёт дифференциальная форма теоремы Гаусса:
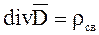
В электротехнических расчётах используют ещё вектор электрической индукции, или вектор электрического смещения:
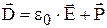 ,
,
где 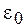 - электрическая постоянная или диэлектрическая проницаемость вакуума, равная
- электрическая постоянная или диэлектрическая проницаемость вакуума, равная 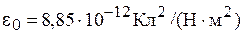 ; - вектор поляризации.
; - вектор поляризации.
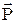 =
= 0Eæ, где æ- диэлектрическая восприимчивость.
0Eæ, где æ- диэлектрическая восприимчивость.
Смысл введения вектора электрической индукции состоит в том, что поток вектора  через любую замкнутую поверхность определяется только свободными зарядами, а не всеми зарядами внутри объёма, ограниченного данной поверхностью, подобно потоку вектора
через любую замкнутую поверхность определяется только свободными зарядами, а не всеми зарядами внутри объёма, ограниченного данной поверхностью, подобно потоку вектора 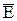 .
.
Уравнения Пуассона и Лапласа являются основными дифференциальными уравнениями электростатики. Они вытекают из теоремы Гаусса в дифференциальной форме. Учитывая, что 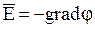 (вместо
(вместо 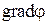 запишем его эквивалент
запишем его эквивалент  ; вместо div напишем
; вместо div напишем 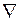 ) и
) и  получим:
получим:
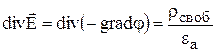 ,
,
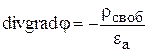 .
.
Вместо  запишем его эквивалент
запишем его эквивалент 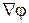 ; вместо div напишем
; вместо div напишем  :
:
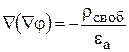
или
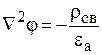
Это уравнение называют уравнением Пуассона. Частный вид уравнения Пуассона, когда 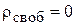 , называют уравнением Лапласа:
, называют уравнением Лапласа:
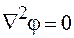
Оператор  называют оператором Лапласа или лапласианом.
называют оператором Лапласа или лапласианом.
Раскрыв 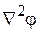 в декартовой системе координат уравнение Пуассона примет вид:
в декартовой системе координат уравнение Пуассона примет вид:


Уравнение Пуассона в декартовой системе координат:

Уравнение Лапласа в декартовой системе координат:

Итак, уравнение Пуассона дает связь между частными производными второго порядка от  в любой точке поля и объемной плотностью свободных зарядов в этой точке поля. Потенциал в этой точке поля зависит от всех видов заряда, создающих поле, а не только от величины свободных зарядов.
в любой точке поля и объемной плотностью свободных зарядов в этой точке поля. Потенциал в этой точке поля зависит от всех видов заряда, создающих поле, а не только от величины свободных зарядов.
В общем случае:
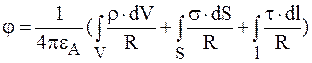 .
.
Используя данную формулу, следует учитывать, что потенциал на бесконечности равен нулю; заряды, создающие поле расположены в ограниченной области.
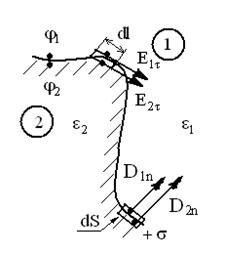
Граничные условия в электростатике. При решении задач электродинамике нужно знать, какими зависимостями связанны между собой компоненты векторов поля и потенциалы на границах разделов сред с различными физическими свойствами. На рис.6 изображена в общем виде криволинейная граница раздела сред 1 и 2 с диэлектрическими постоянными  и
и 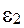 .
.
 |
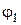 и
и  – потенциалы;
– потенциалы;
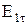 и
и 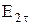 – касательные составляющие вектора Е;
– касательные составляющие вектора Е;
D1n и D2n – нормальные компоненты вектора смещения D в точках, примыкающих к границе в одном месте, но с разных сторон
В общем случае на границе с поверхностной плотностью  (К/м2) может быть распределен заряд. Если далее воспользоваться теоремой Гаусса и принципом потенциальности в интегральной форме
(К/м2) может быть распределен заряд. Если далее воспользоваться теоремой Гаусса и принципом потенциальности в интегральной форме
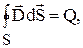

можно показать, что:
1.На границе раздела двух сред непрерывны тангенциальные составляющие вектора напряженности  .
.
2. Нормальная составляющая вектора  скачком изменяется на величину, равную поверхностной плотности свободных зарядов на границе раздела сред
скачком изменяется на величину, равную поверхностной плотности свободных зарядов на границе раздела сред
 ;
;
3. при переходе через границу раздела двух сред потенциал остается непрерывным
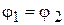 .
.
Эти связи называютграничными условиями электростатики.
Лекция 3
|
|
|
|
|
Дата добавления: 2014-10-22; Просмотров: 6219; Нарушение авторских прав?; Мы поможем в написании вашей работы!