Первый закон Кирхгофа в дифференциальной форме

Закон Ома в дифференциальной и интегральной форме.

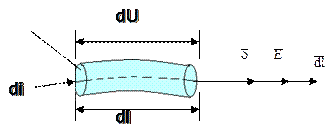
Если в стационарном поле тока выделить трубку тока (рис. 7), то, с одной стороны, напряжение на трубке будет равно

du=Edl,

а с другой — по закону Ома:

,

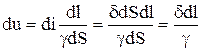где 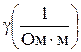– удельная проводимость среды.

.

Отсюда следует, что

.

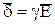Это выражение называют законом Ома в дифференциальной форме.

Как было сказано выше, в общем случае

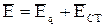
и, исходя из этого, может быть получен обобщенный закон Ома в дифференциальной форме:

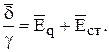
Интегрирование уравнения

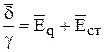
по пути l (рис.8) приводит к следующему выражению:

.

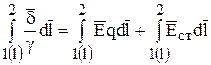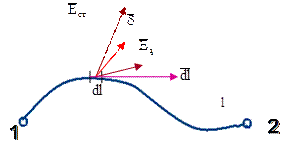
Рис.8

Первый интеграл справа — напряжение между точками 1 и 2, обусловленное кулоновскими полями и не зависящее от формы пути l. Второй интеграл — ЭДС участка 1—2 по пути l. Следовательно, обобщенный закон Ома в интегральной форме принимает вид:

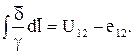
Если в проводящей среде выделить некоторый объём, по которому протекает постоянный ток, то можно сказать, что ток, который войдёт в объём, должен равняться току, вышедшему из объёма, иначе в этом объёме происходило бы накопление электрических зарядов, что опыт не подтверждает. Сумму входящего в объём и выходящего из объёма токов записывают так:

.

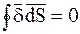Если разделить левую и правую части этого уравнения на одно и то же число, то равенство останется справедливым:

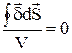
Очевидно, что последнее соотношение будет справедливо и в том случае, если объём, находящийся внутри замкнутой поверхности, устремим к нулю:

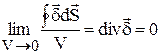
Для постоянного поля в проводящей среде

.

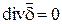Это соотношение называют первым законом Кирхгофа в дифференциальной форме. Оно означает, что в установившемся режиме (при постоянном токе) в любой точке поля нет ни истока, ни стока линий тока проводимости .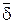

Второй закон Кирхгофа для квазилинейного проводника.

Интегрирование выражения

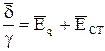
по замкнутому контуру с учетом того, что

,

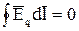приводит к выражению, известному как второй закон Кирхгофа:

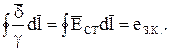
Если замкнутый контур состоит из n квазилинейных проводников, характеризующихся параметрами , то с учетом изложенного выше

,

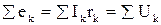как это и принимается в теории цепей постоянного тока.

Алгебраическая сумма ЭДС замкнутого контура равна алгебраической сумме напряжений на сопротивлениях этого контура. Как и ранее, следует иметь в виду, что если направления ЭДС (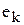) и тока (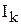) совпадают с направлением обхода контура, то соответствующие слагаемые в уравнении Кирхгофа положительны, а если не совпадают — отрицательны.

Дата добавления: 2014-10-22