Геометрические характеристики поперечных сечений бруса

2.1 Основные определения

При решении задач сопротивления материалов возникает необходимость оперировать определенными геометрическими характерис-тиками поперечных сечений бруса. В силу своего узкого прикладного значения в общем курсе геометрии они не изучаются.

А

Рассмотрим некоторое поперечное сечение бруса площадью А в системе координат х,у (рис.2. 1 ). Интегралы

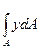S_х=и S_y=

называются статическими моментами площади поперечного сечения. Здесь dA – элементарная часть рассматриваемой площади (элементарная площадка) с координатами х,у. Размерность статического момента сечения [м³] или [см³]. Он может быть больше нуля, меньше нуля или равен нулю.

Если известны координаты центра тяжести сечения и его площадь, то статические моменты определятся по формулам

S_х= y_c А·, S_Y = x_с А,

из которых следуют выражения для определения координат центра тяжести

y_с= , x_с= .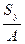

Интегралы

І_х =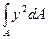, І_у =

называются осевыми моментами инерции сечения относительно соответственно осей х и у

Интеграл

І_ху =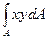

называется центробежным моментом инерции сечения относительно осей х, у

Интеграл

І_ρ =

называется полярным моментом инерции сечения.

Размерность рассмотренных моментов инерции [м⁴] или [см^4]].

Так как ρ² = у² + х² ,тоІ_ρ = = , таким образом,

І_ρ = І_х + І_у .

Осевые и полярный моменты инерции всегда положительны, центробежный момент инерции может быть положительным, отрицательным или равным нулю.

Отношение осевого момента инерции к ординате наиболее удаленной от оси точки называется моментом сопротивления при изгибе: 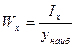-момент сопротивления при изгибе относительно оси х, - момент сопротивления при изгибе относительно оси у.

Отношение полярного момента инерции к радиусу наиболее удаленной точки от начала координат называется полярным моментом сопротивления или моментом сопротивления при кручении.

Дата добавления: 2014-10-23