Зависимость между моментами инерции относительно

Геометрические характеристики простейших фигур

Рассмотрим геометрические характеристики прямоугольника, треугольника, круга и кольца.

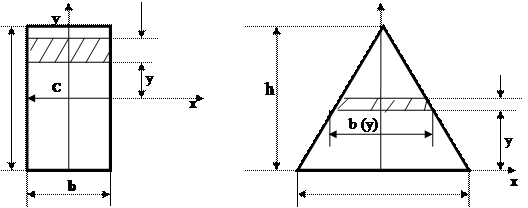
Прямоугольник: выделим элементарную площадку dA ═ b·dy (рис.2.2). Тогда

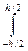І_х = у² dA = 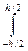у² b dy = у³ b ∕ 12| 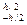= bh³ ∕ 12.

dy

h

у  

Рис.2.3

Рис.2.2

dy  

b

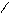
Треугольни к: элементарная площадка запишется выражением dA═b(у)·dy (рис.2.3). Из подобия треугольников следует b(у) ∕ b = (h─y) ∕ h, откуда получим

b(у) =b(1- 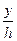), І_х = 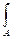у² dA =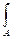у² b(1- 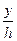) ·dy = b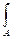(у² – 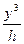) dy = b(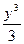– 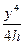)|= bh³ ∕ 12.

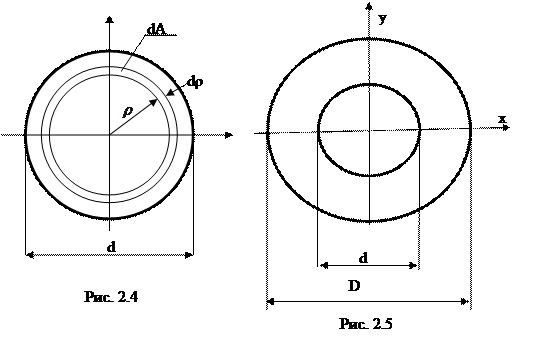Круг: выделим элементарную площадку dA (рис.2.4) в виде кольца с радиусами ρ и ρ+dρ, т.е., dA=2πρdρ.

Полярный момент инерции І_ρ ═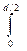ρ²dA ═ 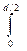ρ²2πρdρ ═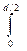2πρ³dρ ═2πρ⁴ ∕ 4|═

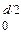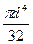
Так как І_ρ = І_х + I_y, а для круга І _х ═ І_y, тоІ_х═ І_y═ .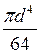

Кольцо: моменты инерции кольц а с диаметрами D и d (рис. 2.5)определятся как разница моментов инерции круга с диаметром D и круга с диаметром d

І_х = І_у =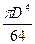– 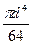= 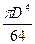( 1- ).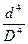

Введем обозначение 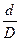═ α , тогда

І_х = І_у =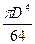( 1 – α⁴ ), І _ρ= 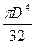(1 – α⁴).

x₁

параллельных осей, одни их которых центральные

Для произвольного сечения, представленного на рис. 2.6, проведем центральные оси x, y, относительно которых S_х = Sу = 0, а затем параллельные им оси Х₁, У₁. Координаты центра тяжести в этих осях обозначим через 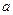и b, тогдакоординаты элементарной площадки dA будутх₁ =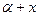, у₁ =.

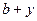Рассмотрим осевой момент инерции относительно оси Х₁:

Рис.2.6  

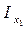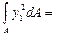
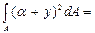
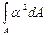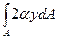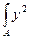= + +dA.

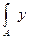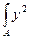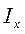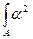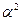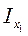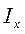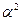Так как dA = S_х = 0, dA = , dA = А, то = + А,

Аналогично 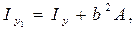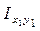═ 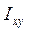+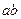А.

Таким образом, осевые моменты инерции относительно произвольных осей, параллельных центральным, находятся как сумма моментов инерции относительно центральных осей и произведения площади сечения на квадрат расстояния между осями, центробежный момент инерции – как сумма центробежного момента инерции относительно центральных осей и произведения площади сечения на расстояния между осями.

Дата добавления: 2014-10-23