Вычисление моментов инерции относительно центральных осей X,Y

Размеры и геометрические характеристики элементов заданного сечения

Решение

Из справочных данных выпишем необходимые для расчетов размеры и геометрические характеристики элементов заданного сечения.

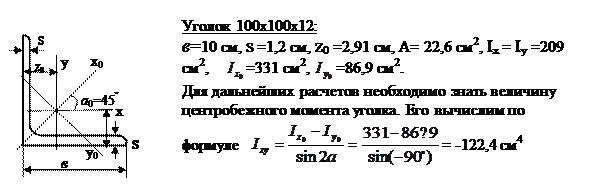
произвольные оси u,v, параллельные центральным осям элементов и определим в этих осях координаты центров тяжестей c₁ и c₂ :

см,

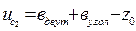=9+10-2,91=16,09 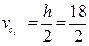см,

см,

=18 - 2,91 = 15,09 см.

Учитывая, что геометрические характеристики сложного сечения находятся как сумма геометрических характеристик элементов, составляющих данное сечение, то координаты центра тяжести сечения вычислим по формулам

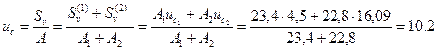см,

см.

По найденным координатамотметим на чертеже сечения его центр тяжести с, проведём через него центральные оси х,у, параллельные центральным осям элементов, и вычислим относительно их моменты инерции, используя формулы преобразования моментов инерции при параллельном переносе осей, одни из которых центральные:

;

;

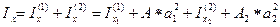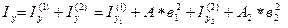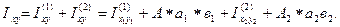
Здесь: a ₁, в ₁ –расстояния между центральной осью сечения х центральными осями элементов сечения х₁ и х₂;

a ₂, в ₂ - – расстояния между центральной осью сечения у и центральными осями элементов сечения у₁ и у₂.

Рис. 2.14

Из чертежа 2.14 следует: см, см,

см, см.

Осевые моменты инерции первого элемента (двутавра) относительно собственных центральных осей x₁,y₁: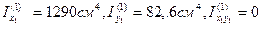

Осевые моменты инерции второго элемента (уголка) относительно собственных центральных осей х₂,у₂: .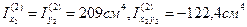

С учетом записанных формул и значений моментов инерции относительно собственных центральных осей получим:

I_х=1290+23,4*(-3)²+209+22,8*(3,09)²=1927,3 см^4,

=82,6+23,4*(-5,7)²+209=22,8*(5,89)²=1804,9 см⁴,

I_ху=0+23,4*(-3)*(-5,7)-122,4+22,8*3,09*5,89=692,7 см⁴.

Дата добавления: 2014-10-23