
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Критической силы
|
|
|
|
Влияние условий закрепления стержня на величину
Формула Эйлера для критической силы
Вывод формулы Эйлера рассмотрим на примере двух опорной балки, нагруженной сжимающей осевой силой F. При F=Fкр балка прогнется. Запишем дифференциальное уравнение изогнутой оси:
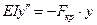 ,
,  .
.
здесь I=Imin.
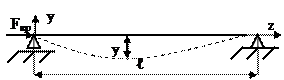
|

 (8.1).
(8.1).
Его решение имеет вид:
 .
.
Значения А и В определятся из граничных условий (z = 0 и z=ℓ). В рассматриваемой балке имеем при z=0 y=0; при z=ℓ y=0. Тогда из (8.1) следует

так как 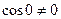 , sinkℓ≠0, то В=0, тогда
, sinkℓ≠0, то В=0, тогда
Asinkℓ=0.
Но A≠0, так как балка не будет иметь прогибов, поэтому
sinkℓ=0, т.е.kℓ=0, , 2π, 3π,…nπ.
, 2π, 3π,…nπ.
Из последнего равенства находим
k2=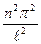 =
= ,
,
откуда следует формула
 ,
,
n≠0, тогда при n=1 получим окончательное выражение для критической силы, называемой формулой Эйлера:
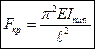 . (8.2)
. (8.2)
Уравнение изогнутой оси стержня при потере устойчивости определится формулой  ., т.е. она представляет собой дугу синусоиды. Для рассмотренного стержня, шарнирно закрепленного по концам (эйлеровский случай), изогнутая ось принимает форму полуволны синусоиды длиной ℓ. Стержень с жестким закреплением при изгибе принимает форму четверти волны синусоиды, а полая полуволна будет располагаться на длине 2ℓ. Для такого стержня критическая сила будет равна
., т.е. она представляет собой дугу синусоиды. Для рассмотренного стержня, шарнирно закрепленного по концам (эйлеровский случай), изогнутая ось принимает форму полуволны синусоиды длиной ℓ. Стержень с жестким закреплением при изгибе принимает форму четверти волны синусоиды, а полая полуволна будет располагаться на длине 2ℓ. Для такого стержня критическая сила будет равна
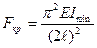 .
.
Для сопоставления критической силы эйлеровского стержня с критической силой стержня, имеющего другие условия закрепления концов, вводится коэффициент приведения длины, который показывает во сколько раз следует изменить длину стержня с заданными ус-
ловиями закрепления по сравнению с длиной стержня с с шарнирно закрепленными концами. Форма изогнутой оси и коэффициенты приведения её длины представлены на рисунке
С учетом рассмотренного коэффициента приведения длины стержня μ критическая сила будет определяться формулой 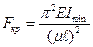 (8.3).
(8.3).
|
|
|
|
|
Дата добавления: 2014-10-23; Просмотров: 761; Нарушение авторских прав?; Мы поможем в написании вашей работы!
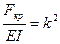 , получим дифференциальное уравнение второго порядка без правой части.
, получим дифференциальное уравнение второго порядка без правой части.