Кручение тонкостенного стержня с замкнутым профилем

Свободное кручение составного открытого профиля

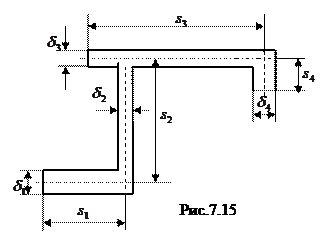Если тонкостенный открытый профиль является составным (рис. 7.15), то поступают следующим образом: крутящий момент в сечении рассматривают как сумму моментов, действующих на отдельных участках; угол поворота отдельных участков равен углу поворота всего сечения, т.е.,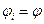. В этом случае согласно формулам (7.17), (7.18)

,

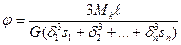. (7.19)

При помощи плёночной аналогии установлено, что максимальные касательные напря-жения возникают на участке с максимальной толщиной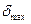. Для этого участка, которому пропишем номер i, также справедливы формулы (7.18), (7.19):

; ,

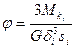где 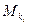- доля крутящего момента, соответствующего i- ому участку; 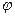- угловое перемеще-ние, единое для всех участков. Исключая из этих выражений 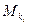, находим

,

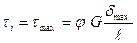учитывая выражение (7.20), получим

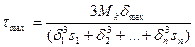(7.20)

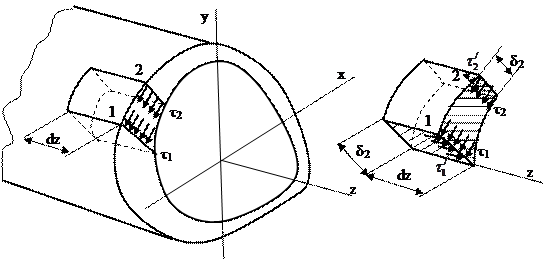
Рассмотрим кручение стержня с поперечным сечением в форме тонкостенного замкнутого профиля (рис.7.16). В этом стержне, в отличие от открытого профиля, напряжения по толщине стенки распределяютя равномерно. Выделим из этого стержня элементарный объём длиной dz, расстояние между точками 1 и 2 которого произвольное. Пусть толщина контура в точке 1 будет δ₁, а в точке 2 – δ₂. Обозначим соответственно через τ₁ и τ₂ напряжения в поперечном сечении. В продольных сечениях будут действовать парные напряжения .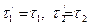

Рис. 7.16

Составим для рассматриваемого элемента уравнение равновесия, спроектировав все силы на направление оси стержня

.

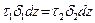Из полученного равенства следует, что τδ = const, так как точки 1 и 2 взяты произвольно. Таким образом, произведение τδ по длине замкнутого контура является величиной постоянной. На участках с меньшей толщиной напряжения будут соответственно бòльшими.

Выразим крутящий момент через напряжения τ. Для этого возьмём на контуре элементарную дугу длиной ds (рис. 7.17). Момент силы τ·δ·ds относительно произвольной точки О равен τδds|ОА|. Тогда

М_к = ∫.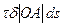

Так как τδ по длине дуги не изменяется, то получим

М_к = τδ ∫.

Выражение 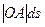представляет собой удвоенную площадь треугольника ОВС, а интеграл от этого произведения по длине замкнутого контура даёт удвоенную площадь, ограниченную средней линией контура. Обозначим эту площадь через F^*. Таким образом,

М_к = τδ2 F^*.

наибольшее напряжение

.

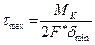Для определения углового перемещения φ рассмотрим соотношение потенциальной энергии, выраженной через напряжения τ и выраженной через внешний момент М. Удельная потенциальная энергия при сдвиге определяется выражением

.

Энергия, накопленная в элементарном объёме с размерами ds, z, δ равна

dU = .

Это выражение необходимо проинтегрировать по длине стержня и по дуге замкнутого контура

U = .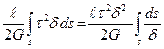

Последний интеграл зависит от закона изменения толщины по дуге контура и является геометрической характеристикой сечения. Учитывая, что

τδ =

Получим

U = .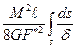

Теперь эту же энергию найдём как работу внешнего момента М на угловом перемещении φ:

U= .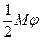

Из равенства этих двух выражений находим

.

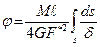Если толщина δ по дуге контура не меняется, то

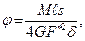
где s - длина замкнутого контура.

Для рассмотренного тонкостенного замкнутого профиля вводятся геометрические параметры W_k, I_k, которые согласно полученным формулам для вычислений напряжений углов поворотов определятся выражениями:

.

Теперь формулы для вычислений напряжений углов поворотов примут вид:

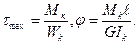
Контрольные вопросы

1. Когда брус испытывает кручение?

2. Что называется валом?

3. Какие внутренние усилия действуют в поперечном сечении вала? Как они

определяются?

4. Какие напряжения действуют в поперечном сечении вала?

5. Как определяются максимальные напряжения в поперечном сечении вала?

5. Условие прочности при кручении вала?

6. Какие перемещения возникают в вале при кручении и как они определяются?

7. Как определяется жёсткость при кручении вала?

Дата добавления: 2014-10-23