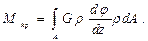КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
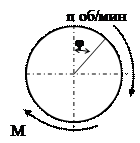
Напряжения и деформации при кручении круглого вала
|
|
|
|
Мощностью и числом оборотов вала
Связь между моментом внешних пар сил, передаваемой
Обычно известны передаваемая мощность N и число оборотов вала n.
 Мощность - это работа внешних сил за единицу времени:
Мощность - это работа внешних сил за единицу времени: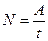 . При кручении вала работа определяется произведением величины внешнего момента М на угол поворота φ, т.е.,
. При кручении вала работа определяется произведением величины внешнего момента М на угол поворота φ, т.е., 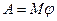 ,
, 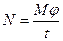 , но
, но 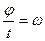 -угловая скорость, следовательно, N= Мω.Угловая скорость определится по формуле
-угловая скорость, следовательно, N= Мω.Угловая скорость определится по формуле 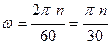 , с учётом которой момент определится из выражения
, с учётом которой момент определится из выражения
М= 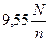 . (7.4).
. (7.4).
Здесь N – передаваемая валом мощность 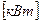 , n – число оборотов вала в минуту, М – внешний момент на валу
, n – число оборотов вала в минуту, М – внешний момент на валу 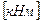 .
.
Расчет на прочность и жёсткость
Рассмотрим брус круглого сечения, нагруженный парами сил в плоскости торцевого сечения (рис.7.7). В поперечных сечениях этого бруса возникает постоянный крутящий.момент 
мя сечениями в процессе деформации кручения не изменяется (εz = 0);
3) поперечные сечения в своей плоскости не деформируются, т.е., радиусы не искривляются и не изменяют своей длины, они лишь поворачиваются как жесткие диски (εх=0, εу=0).
На основании этих допущений σх =σу =σz =τху =0, поэтому в поперечных сечениях будут действовать только касательные напряжения τzx и τzу, следовательно, при кручении брус испытывает деформацию чистого сдвига.
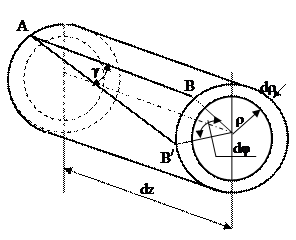
Двумя поперечными сечениями выделим из вала элемент длиной dz, а из него затем выделим элементарное кольцо с радиусами ρ и ρ + dρ (рис. 7.8). Будем считать левое торцевое сечение неподвижным, тогда правое торцевое сечение кольца повернется под действием крутящего момента относительно левого на угол dφ. Образующая цилиндра АВ при этом повернётся на угол γ и займет положение 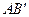 . С одной стороны дуга
. С одной стороны дуга 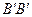 / =ρdφ, с другой - В/ В/ = γdz, следовательно,
/ =ρdφ, с другой - В/ В/ = γdz, следовательно,
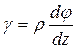 . (7.6)
. (7.6)
Угол γ – это угол сдвига цилиндрической поверхности, а величина 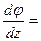 Θ называется относительным углом закручивания (аналогично
Θ называется относительным углом закручивания (аналогично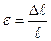 ).
).
|
|
Так как 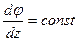 , то
, то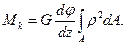 Учитывая, что
Учитывая, что 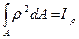 получим
получим
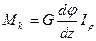 ,
,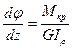 (а),
(а), 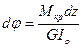 .
.
Из последнего выражения следует формула угла закручивания
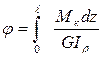 (7.8)
(7.8)
Если крутящий момент Мк и жесткость вала GІρ по его длине не изменяются, то
|
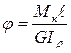 (7.9)
(7.9) Вернёмся к выражению (7.7). Используя уравнение (а), получим формулу касательных напряжений при кручении круглого вала
Вернёмся к выражению (7.7). Используя уравнение (а), получим формулу касательных напряжений при кручении круглого вала
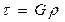
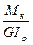 =
=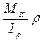 (7.10)
(7.10)
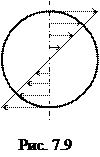
Согласно этой формуле касательные напряжения в поперечном сечении вала распределяются вдоль радиуса по линейному закону, достигая наибольшей величины в точке наиболее удаленной от оси бруса (рис.7.9).
Согласно (7.10): 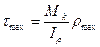 или
или 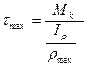 .
.
Введя обозначение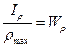 (момент сопротивления сечения при кручении), получим
(момент сопротивления сечения при кручении), получим
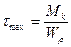 .
.
Для круглого сечения 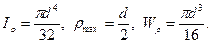
Материал вала возле оси недогружен, поэтому применяют пустотелые валы. При равных площадях поперечных сечений и одинаковом крутящем моменте в пустотелом вале напряжения будут меньше, а при равных напряжениях в пустотелом вале крутящий момент будет больше.
Для такого вала 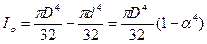 ,
,
где D- наружный диаметр, d – внутренний диаметр вала,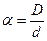 ,
,
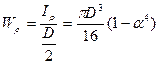 .
.
Расчёт на прочность круглого вала может выполняться по двум методам: по допус-каемым напряжениям и по допускаемым нагрузкам. В данном разделе рассмотрим первый метод- метод допускаемых напряжений, так как он наиболее часто используется на практике.
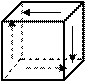
|
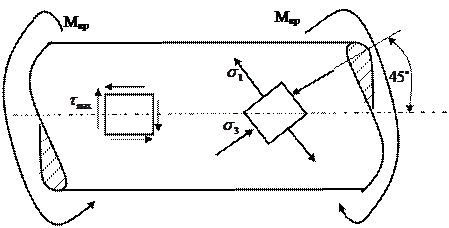 Предельное состо-яние в опасной точке, расположенной на повер-хности вала (рис.7.10) достигается в сечении с наибольшим крутящим моментом. В этой точке будет напряжённое сос-тояние чистого сдвига, т.е. по граням элементарного параллелепипеда действу-ют только касательные напряжения (рис.7.11). В этом случае
Предельное состо-яние в опасной точке, расположенной на повер-хности вала (рис.7.10) достигается в сечении с наибольшим крутящим моментом. В этой точке будет напряжённое сос-тояние чистого сдвига, т.е. по граням элементарного параллелепипеда действу-ют только касательные напряжения (рис.7.11). В этом случае 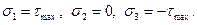
|
состояния определяется выражением
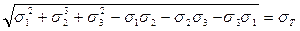 .
.
Для рассматриваемого случая оно примет вид 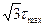 =
=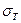 .
.
Для безопасной работы вала должно выполняться условие 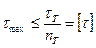 ,т.е.
,т.е.
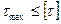 , где
, где 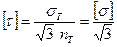 .
.
Таким образом, условие прочности при кручении круглого вала запишется формулой:
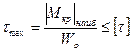 . (7.11)
. (7.11)
Из него следуют формулы для назначения размеров поперечного сечения вала и определения грузоподъёмности:
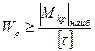 ,
,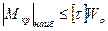 (7.12)
(7.12)
Условие жесткости 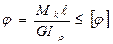 . (7.13)
. (7.13)
Произведение GIρ называется жесткостью при кручении. Іρ – полярный момент инерции, G – модуль упругости при сдвиге.
Если вал имеет несколько участков, то угол закручивания φ на всей его длине найдется как сумма углов закручивания на всех участках φi:
φ =∑ φi =∑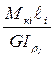 (7.14)
(7.14)
Пример: подобрать размеры круглого и кольцевого сечения вала, передающего мощ-ность 80 кВт при числе оборотов n=600об/мин, если 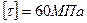 , α =
, α =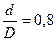 . Сравнить массы валов с указанными сечениями.
. Сравнить массы валов с указанными сечениями.
Мк = 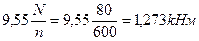 ,
, 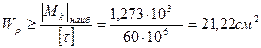 .
.
Для круглого сечения: 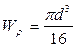 , тогда
, тогда 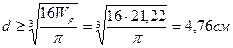 ,
,
площадь сечения А = 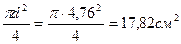 .
.
Для кольцевого сечения: 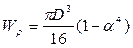 ,
, 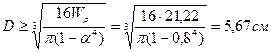 ,
,
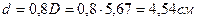 , площадь сечения А=
, площадь сечения А=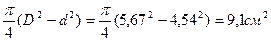 .
.
Массы валов будут пропорциональны площадям поперечных сечений 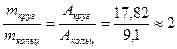 , т.е., полый вал будет почти в два раза легче сплошного вала.
, т.е., полый вал будет почти в два раза легче сплошного вала.
|
|
|
|
|
Дата добавления: 2014-10-23; Просмотров: 581; Нарушение авторских прав?; Мы поможем в написании вашей работы!
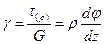 ,
откуда следует
,
откуда следует
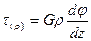 (7.7)
Подставляя (7.7) в уравнение (7.5), получим
(7.7)
Подставляя (7.7) в уравнение (7.5), получим